Предмет: Математика,
автор: Aibolit123
уравнение геометрического места точек на плоскости oxy равноудаленных от точек А(-2,5) и B(3,-6) имеет вид
1)5x-11y-8=0
2)5x-11y+8=0
3)11x-5y-8=0
4)11x+5y-8=0
5)5x+11y+8+0
Ответы
Автор ответа:
1
решение на фото ниже, ответ выбери сам:
Приложения:
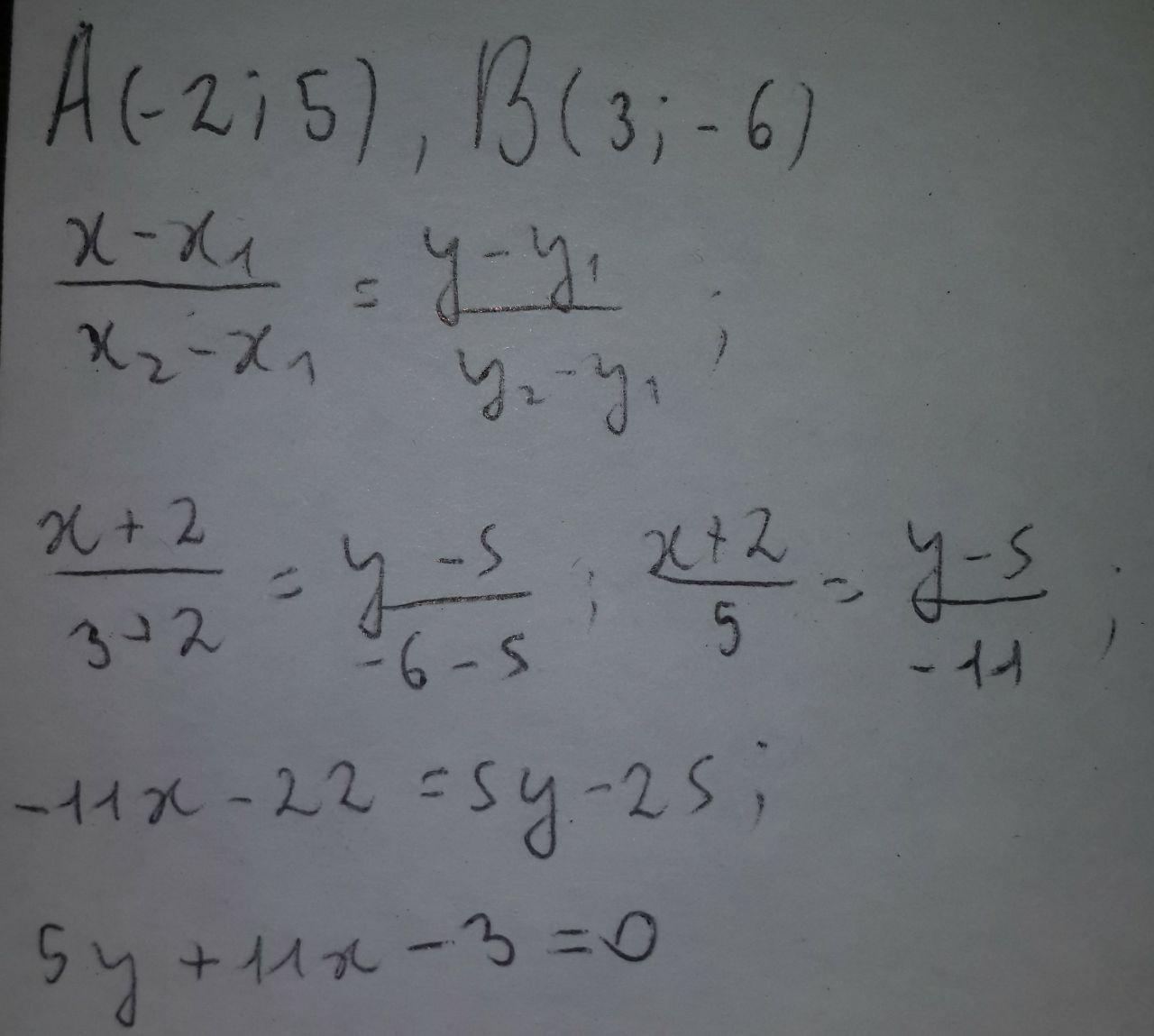
Автор ответа:
3
А(-2; 5)
В(3; - 6)
Пусть некоторая точка К(х; у), удовлетворяющая данному условию, имеет координаты (х; у), тогда расстояния АК и ВК равны:
|AK| = |BK|
|AK|² = (x - (-2))² + (y - 5)²
|BK|² = (x - 3)² + (y - (-6))²
Т.к. |AK| = |BK|, то
(x - (-2))² + (y - 5)² = (x - 3)² + (y - (-6))²
(х+2)² + (у - 5)² = (х - 3)² + (у + 6)²
х² + 4х + 4 + у² - 10у + 25 = х² - 6х + 9 + у² + 12у + 36
4х - 10у + 29 = - 6х +12у + 45
4х + 6х - 10у -12у + 29 - 45 = 0
10х - 22у - 16 = 0
Разделив обе части уравнения на 2, получим:
5х - 11у - 8 = 0
Ответ под цифрой 1) 5х - 11у - 8 = 0
В(3; - 6)
Пусть некоторая точка К(х; у), удовлетворяющая данному условию, имеет координаты (х; у), тогда расстояния АК и ВК равны:
|AK| = |BK|
|AK|² = (x - (-2))² + (y - 5)²
|BK|² = (x - 3)² + (y - (-6))²
Т.к. |AK| = |BK|, то
(x - (-2))² + (y - 5)² = (x - 3)² + (y - (-6))²
(х+2)² + (у - 5)² = (х - 3)² + (у + 6)²
х² + 4х + 4 + у² - 10у + 25 = х² - 6х + 9 + у² + 12у + 36
4х - 10у + 29 = - 6х +12у + 45
4х + 6х - 10у -12у + 29 - 45 = 0
10х - 22у - 16 = 0
Разделив обе части уравнения на 2, получим:
5х - 11у - 8 = 0
Ответ под цифрой 1) 5х - 11у - 8 = 0
Похожие вопросы
Предмет: История,
автор: Loool7788
Предмет: История,
автор: annagorodnyanina
Предмет: Физика,
автор: anastejsha7
Предмет: Математика,
автор: rustamov23
Предмет: Обществознание,
автор: dddddfjjg