Предмет: Алгебра,
автор: lubov199718
Решите пожалуйста,желательно с объяснениями что откуда взялось
Приложения:
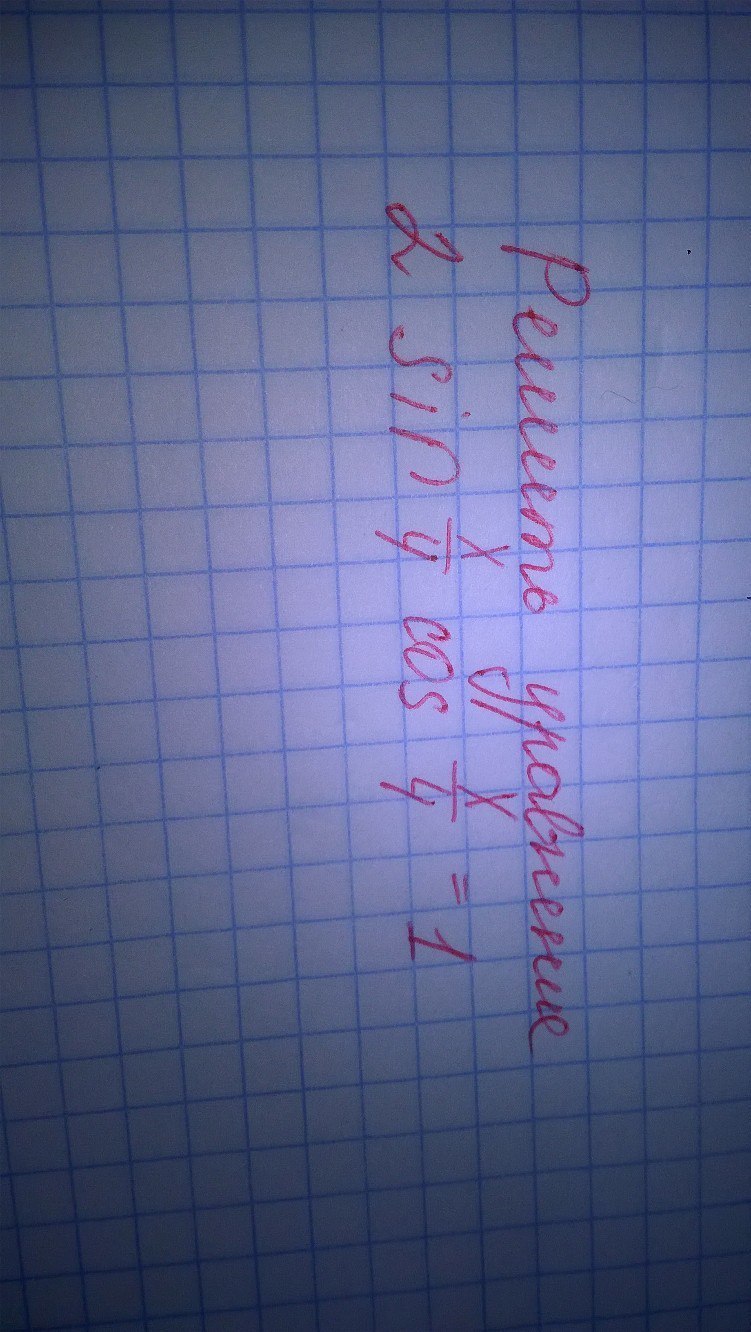
Ответы
Автор ответа:
0
по формуле: 

далее по правилу оформления решений тригонометрических уравнений последовательно получаем:





далее по правилу оформления решений тригонометрических уравнений последовательно получаем:
drwnd:
получилось бы -(sina+cosa)^2 = 0; если Вы хотели извлечь корень из обоих частей, то Вы бы столкнулись с извлечением корня из отрицательного выражения, что, увы, здесь недозволительно
Нет, почему же?
2sinxcosx=sin^2x + cos^2x
sin^2x - 2sinxcosx + cos^2x = 0
(sinx - cosx)^2=0
зачем так сложно? я сделал проще)
Мне кажется, что хорошо обратить внимание и на такую возможность, поскольку можно забыть ту или иную формулу и решить в лоб
а когда Вы переносите в левую часть Вашу преобразованную единицу, что у вас получается?
и, соглашусь с AnonimusPro, к чему усложнять решение
Я же расписал выше что получается. Ну и не думал, что формула сокращенного умножения - это усложнять.
Автор ответа:
0
2sin(x/4)*cos(x/4)=1
sin(x/2)=1
x/2=pi/2+2pi*n
x=pi+4pi*n
Ответ: x=pi+4pi*n
sin(x/2)=1
x/2=pi/2+2pi*n
x=pi+4pi*n
Ответ: x=pi+4pi*n
Похожие вопросы
Предмет: История,
автор: Butterflyxs
Предмет: Физика,
автор: annkarpenko6
Предмет: Английский язык,
автор: yuliannakh11
Предмет: Русский язык,
автор: naskadyach2015
Предмет: Английский язык,
автор: pedrodolimi