Предмет: Математика,
автор: dimaxt79
Вычислить определенные интегралы:
Приложения:
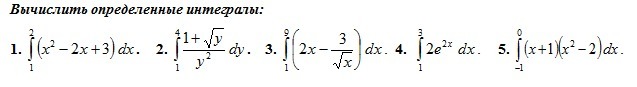
Ответы
Автор ответа:
2
1. Сначала нахоим неопределённый интеграл
∫(x^2 - 2x + 3) dx = (1/3) x^3 - x^2 + 3x +C
Теперь считаем определённый, подставляя пределы интегрирования:
∫ = (1/3) * 2^3 - 2^2 + 3*2 - ((1/3) * 1^3 - 1^2 + 3*1) = 8/3 +2 - (1/3 + 2) = 7/3
2. ∫((1 + √y) / y^2) dy = ∫ dy / y^2 + ∫ y^(-3/2) dy = -1/y - 2y^(-1/2) + C
∫ = -1/4 - 2 * 4^(-1/2) - (-1/1 - 2 * 1^(-1/2)) = -1/4 - 1 - (-1 - 2) = 7/4
3. ∫(2x - 3/√x) dx = x^2 - 6x^(1/2) + C
∫ = 9^2 - 6*9^(1/2) - (1^2 - 6*1^(1/2)) = 81 - 18 - (1 - 6) = 68
4. ∫2e^(2x) dx = ∫ e^(2x) d(2x) = e^(2x) + C
∫ = e^(2*3) - e^(2*1) = e^4 - e^2 = e^2 (e^2 - 1) ≈ 396.04
5. ∫(x + 1)(x^2 - 2) dx = ∫(x^3 + x^2 - 2x -2) dx = (1/4)x^4 + (1/3)x^3 - x^2 - 2x + C
∫ = (1/4)*0^4 + (1/3)*0^3 - 0^2 - 2*0 - ((1/4)*(-1)^4 + (1/3)*(-1)^3 - (-1)^2 - 2*(-1) = 0 - (1/4 - 1/3 - 1 + 2) = - (-1/12 + 1) = -11/12
∫(x^2 - 2x + 3) dx = (1/3) x^3 - x^2 + 3x +C
Теперь считаем определённый, подставляя пределы интегрирования:
∫ = (1/3) * 2^3 - 2^2 + 3*2 - ((1/3) * 1^3 - 1^2 + 3*1) = 8/3 +2 - (1/3 + 2) = 7/3
2. ∫((1 + √y) / y^2) dy = ∫ dy / y^2 + ∫ y^(-3/2) dy = -1/y - 2y^(-1/2) + C
∫ = -1/4 - 2 * 4^(-1/2) - (-1/1 - 2 * 1^(-1/2)) = -1/4 - 1 - (-1 - 2) = 7/4
3. ∫(2x - 3/√x) dx = x^2 - 6x^(1/2) + C
∫ = 9^2 - 6*9^(1/2) - (1^2 - 6*1^(1/2)) = 81 - 18 - (1 - 6) = 68
4. ∫2e^(2x) dx = ∫ e^(2x) d(2x) = e^(2x) + C
∫ = e^(2*3) - e^(2*1) = e^4 - e^2 = e^2 (e^2 - 1) ≈ 396.04
5. ∫(x + 1)(x^2 - 2) dx = ∫(x^3 + x^2 - 2x -2) dx = (1/4)x^4 + (1/3)x^3 - x^2 - 2x + C
∫ = (1/4)*0^4 + (1/3)*0^3 - 0^2 - 2*0 - ((1/4)*(-1)^4 + (1/3)*(-1)^3 - (-1)^2 - 2*(-1) = 0 - (1/4 - 1/3 - 1 + 2) = - (-1/12 + 1) = -11/12
Похожие вопросы
Предмет: Химия,
автор: samiliar1090
Предмет: Геометрия,
автор: ostmax2001
Предмет: Физкультура и спорт,
автор: egorsyd2011
Предмет: География,
автор: fdhhhfh
Предмет: ОБЖ,
автор: valui4ka4