Предмет: Математика,
автор: filadelfii
Помогите решить три математические задачи!
Приложения:

Ответы
Автор ответа:
1
3) Их должны были высадить за x часов, по 300/x штук в час.
А если сажать в час на 5 больше, то есть 300/x + 5 = (5x+300)/x,
то работа будет завершена на 10 часов раньше, то есть за x-10 часов.
(5x+300)(x-10)/x = 300
5x^2 + 300x - 50x - 3000 = 300x
5x^2 - 50x - 3000 = 0
x^2 - 10x - 600 = 0
(x - 30)(x + 20) = 0
x = -20 < 0 - не подходит
x = 30 часов было запланировано на посадку тюльпанов.
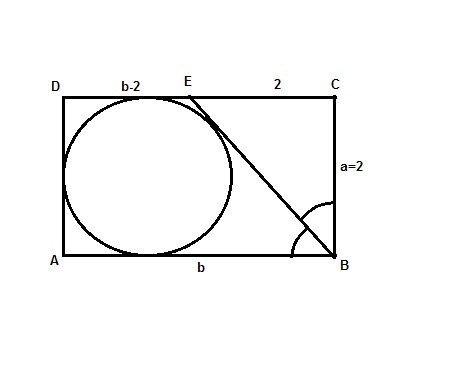
4) Чертеж к задаче на рисунке.
Стороны прямоугольника a = 2R = 2 см и b см - пока неизвестно.
Площадь S(ABCD) = ab = 2b = ??? - нужно найти
ABED - прямоугольная трапеция.
ABE + CBE = 2*ABE = 90°, ABE = CBE = CEB = 45°
Треугольник BCE - прямоугольный и равнобедренный.
CB = CE = 2*R = 2 см; DE = b - 2 см.
S(BCE) = 2*2/2 = 2 кв.см.
Площадь трапеции S(ABED) = b*(b - 2)*a/2 = b(b - 2)*2/2 = b^2 - 2b.
Но, с другой стороны, площадь прямоугольника
S(ABCD) = S(ABED) + S(BCE)
2b = b^2 - 2b + 2
b^2 - 4b + 2 = 0
D = 4^2 - 4*2 = 16 - 8 = 8
b1 = (4 - √8)/2 = (4 - 2√2)/2 = 2 - √2 < 2 - не подходит.
b2 = (4 + √8)/2 = (4 + 2√2)/2 = 2 + √2 - подходит
S(ABCD) = 2b = 2(2 + √2) = 4 + 2√2 = 4 + √8 кв.см.
5)
Область определения:
{ 4x > 0; 4x ≠ 1
{ 2sin(3x)*cos(x) - sin(4x) > 0
Получаем
x ≠ 0; x ≠ 1/4
2 условие будет выполнено, по свойствам логарифмов:
Логарифм от 1 по любому основанию равен 0.
2sin(3x)*cos(x) - sin(4x) = 1
Раскладываем синусы кратных углов:
sin 2a = 2sin a*cos a
sin 3a = sin (a+2a) = sin a*cos 2a + cos a*sin 2a =
= sin a*(1 - 2sin^2 a) + cos a*2sin a*cos a = sin a*(1 - 2sin^2 a + 2cos^2 a) =
= sin a*(1 - 2sin^2 a + 2 - 2sin^2 a) = sin a*(3 - 4sin^2 a)
sin 4a = 2sin 2a*cos 2a = 2sin 2a*(1 - 2sin^2 a)
Подставляем
2sin x(3 - 4sin^2 x)*cos x - 2sin 2x*(1 - 2sin^2 x) = 1
sin 2x*(3 - 4sin^2 x) - sin 2x*(2 - 4sin^2 x) = 1
sin 2x*(3 - 4sin^2 x - 2 + 4sin^2 x) = sin 2x*1 = 1
2x = pi/2 + 2pi*k
x = pi/4 + pi*k
А если сажать в час на 5 больше, то есть 300/x + 5 = (5x+300)/x,
то работа будет завершена на 10 часов раньше, то есть за x-10 часов.
(5x+300)(x-10)/x = 300
5x^2 + 300x - 50x - 3000 = 300x
5x^2 - 50x - 3000 = 0
x^2 - 10x - 600 = 0
(x - 30)(x + 20) = 0
x = -20 < 0 - не подходит
x = 30 часов было запланировано на посадку тюльпанов.
4) Чертеж к задаче на рисунке.
Стороны прямоугольника a = 2R = 2 см и b см - пока неизвестно.
Площадь S(ABCD) = ab = 2b = ??? - нужно найти
ABED - прямоугольная трапеция.
ABE + CBE = 2*ABE = 90°, ABE = CBE = CEB = 45°
Треугольник BCE - прямоугольный и равнобедренный.
CB = CE = 2*R = 2 см; DE = b - 2 см.
S(BCE) = 2*2/2 = 2 кв.см.
Площадь трапеции S(ABED) = b*(b - 2)*a/2 = b(b - 2)*2/2 = b^2 - 2b.
Но, с другой стороны, площадь прямоугольника
S(ABCD) = S(ABED) + S(BCE)
2b = b^2 - 2b + 2
b^2 - 4b + 2 = 0
D = 4^2 - 4*2 = 16 - 8 = 8
b1 = (4 - √8)/2 = (4 - 2√2)/2 = 2 - √2 < 2 - не подходит.
b2 = (4 + √8)/2 = (4 + 2√2)/2 = 2 + √2 - подходит
S(ABCD) = 2b = 2(2 + √2) = 4 + 2√2 = 4 + √8 кв.см.
5)
Область определения:
{ 4x > 0; 4x ≠ 1
{ 2sin(3x)*cos(x) - sin(4x) > 0
Получаем
x ≠ 0; x ≠ 1/4
2 условие будет выполнено, по свойствам логарифмов:
Логарифм от 1 по любому основанию равен 0.
2sin(3x)*cos(x) - sin(4x) = 1
Раскладываем синусы кратных углов:
sin 2a = 2sin a*cos a
sin 3a = sin (a+2a) = sin a*cos 2a + cos a*sin 2a =
= sin a*(1 - 2sin^2 a) + cos a*2sin a*cos a = sin a*(1 - 2sin^2 a + 2cos^2 a) =
= sin a*(1 - 2sin^2 a + 2 - 2sin^2 a) = sin a*(3 - 4sin^2 a)
sin 4a = 2sin 2a*cos 2a = 2sin 2a*(1 - 2sin^2 a)
Подставляем
2sin x(3 - 4sin^2 x)*cos x - 2sin 2x*(1 - 2sin^2 x) = 1
sin 2x*(3 - 4sin^2 x) - sin 2x*(2 - 4sin^2 x) = 1
sin 2x*(3 - 4sin^2 x - 2 + 4sin^2 x) = sin 2x*1 = 1
2x = pi/2 + 2pi*k
x = pi/4 + pi*k
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: foxf54309
Предмет: Биология,
автор: wwwkatyalapenko13
Предмет: История,
автор: linasnastya
Предмет: Қазақ тiлi,
автор: pasanpatsanov
Предмет: Русский язык,
автор: 666444888q