Предмет: Математика,
автор: ариа111111
-5cos4x=2cos^2x+1 //////////
Приложения:
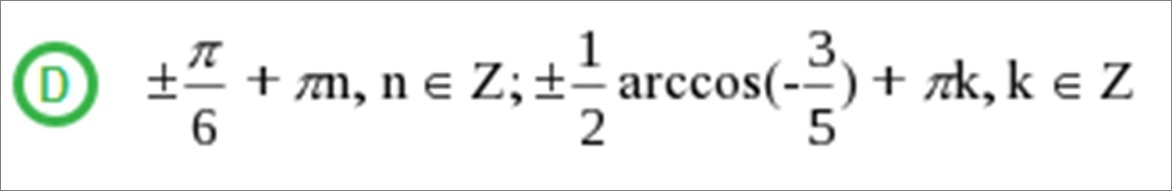
Ответы
Автор ответа:
1
Пусть
D>0, то квадратное уравнение имеет 2 действительных корней
Возвращаемся к замене
Похожие вопросы
Предмет: Биология,
автор: pan59864
Предмет: Қазақ тiлi,
автор: nurali96
Предмет: Математика,
автор: eskapro
Предмет: Русский язык,
автор: Mila12313
Предмет: Русский язык,
автор: Master2133
(это из той же формулы, только теперь двойной угол =4х, а одинарный =2х).
5(cos^{2} {2x}-1)+1+cos2x+1=0\\5cos^22x+cos2x-3=0\\t=cos2x , 5t^2+t-3=0\\D=1+4\cdot 5\cdot 3=61,t_1=\frac{-1-\sqrt{61}}{10}, t_2=\frac{-1+\sqrt{61}}{10}\\2x=\pm arccos\frac{-1-\sqrt{61}}{10}+2\pi n, n\in Z\\x_1=\pm \frac{1}{2}arccos\frac{-1-\sqrt{61}}{10}+\pi n\\x_2=\pm \frac{1}{2}arccos\frac{-1+\sqrt{61}}{10}+\pi k, k