Предмет: Геометрия,
автор: VergoLML
В треугольнике со сторонами AC=14, BC=10, AB=12 проведены биссектрисы АА1 и СС1, точки К и М основания перпендикуляров, опущенных из точки В на прямые АА1 и СС1. Найдите площадь треугольника КВМ.
cos20093:
Легко найти что BK = AB*sin(A/2); BM = BC*sin(C/2); ∠KBM = A/2 + C/2; по смыслу задача уже решена, дальше надо просто выполнить длинные технические действия - по трем сторонам тр-ка ABC найти sin(A/2); sin(C/2) и sin(A/2 + C/2); (последнее - просто по тригонометрическим формулам) и подставить в S = BK*BM*sin(A/2 + C/2)/2;
На самом деле не так все плохо. Всю тригонометрию можно легко свести к сумме синусов углов треугольника ABC
Ну или что-то в этом роде, там не сумма, а (sin(A) + sin(C) - sin(B))/4;
Спасибо)
Ответы
Автор ответа:
1
Высота к AC по формуле Герона:
p= (AB+BC+AC)/2 =18
H= 2√[p(p-AB)(p-BC)(p-AC)]/AC =
= 2√(18*6*8*4)/14 = 24√6/7
В треугольниках BAK1, BCM1 биссектриса является высотой => т. равнобедренные.
CB=CM1
AB=AK1
M1K1= AC-(AC-AK1)-(AC-CM1) = AB+CB-AC = 8
SBK1M1= M1K1*H /2 =4*24√6/7
В равнобедренных т. биссектриса является также медианой => MK соединяет середины BM1 и BK1 => MK - средняя линия BK1M1.
Площадь треугольника, отсекаемого средней линией, равна 1/4 площади исходного.
SBKM = SBK1M1 /4 = 24√6/7 (~8,4)
p= (AB+BC+AC)/2 =18
H= 2√[p(p-AB)(p-BC)(p-AC)]/AC =
= 2√(18*6*8*4)/14 = 24√6/7
В треугольниках BAK1, BCM1 биссектриса является высотой => т. равнобедренные.
CB=CM1
AB=AK1
M1K1= AC-(AC-AK1)-(AC-CM1) = AB+CB-AC = 8
SBK1M1= M1K1*H /2 =4*24√6/7
В равнобедренных т. биссектриса является также медианой => MK соединяет середины BM1 и BK1 => MK - средняя линия BK1M1.
Площадь треугольника, отсекаемого средней линией, равна 1/4 площади исходного.
SBKM = SBK1M1 /4 = 24√6/7 (~8,4)
Приложения:
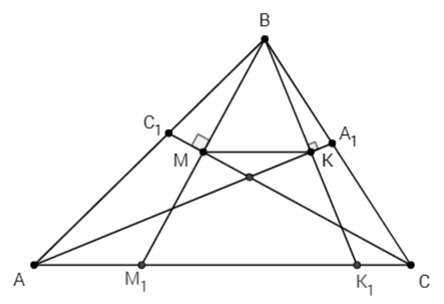
Можно и так. А можно вообще все это не считать - Sbmk = Sbm1k1/4 = (4/7)*Sabc/4 = Sabc/7 (потому что M1K1 = 14 - 2 - 4 = 8; M1K1 = AC*(4/7))
Мне стало интересно, как мой способ дает тот же ответ, там формула уж больно симпатичная получилась
А, ясно, как :) sin(A) = 2S/bc; и так далее :) надо же
Похожие вопросы
Предмет: Математика,
автор: maximjtsapko
Предмет: История,
автор: kssidko11
Предмет: История,
автор: lolil3003
Предмет: Математика,
автор: rifatovarebiya2905
Предмет: Математика,
автор: sabiroffrr