Предмет: Алгебра,
автор: VergoLML
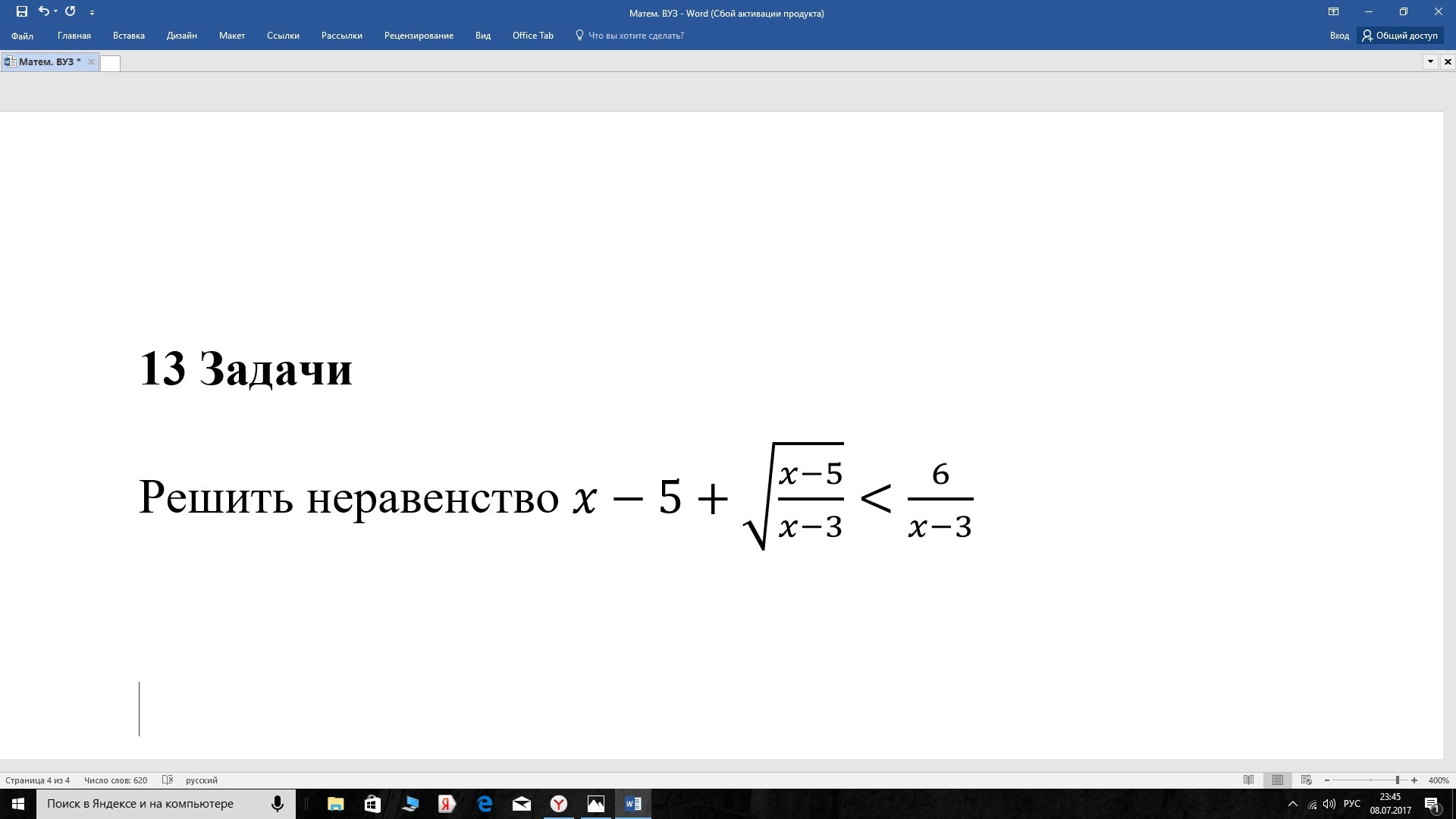
Помогите решить неравенство.
Приложения:
Ответы
Автор ответа:
1
Область определения:
{ x ≠ 3
{ (x-5)/(x-3) >= 0
x ∈ (-oo; 3) U [5; +oo)
Если x < 3, то при умножении на (x-3) знак неравенства поменяется.
Замена
y^2 + y - 6 > 0
(y - 2)(y + 3) > 0
y ∈ (-oo; -3) U (2; +oo), но, так как y > 0, то
y ∈ (2; +oo)
Обратная замена.
x^2 - 8x + 15 > 4
x^2 - 8x + 11 > 0
D/4 = 4^2 - 11 = 16 - 11 = 5
x1 = 4 - √5 ~ 1,764 < 3
x2 = 4 + √5 ~ 6,236 > 3
x ∈ (-oo; 4-√5) U (4+√5; +oo), но x < 3, поэтому
x ∈ (-oo; 4-√5) - ЭТО РЕШЕНИЕ
Если x >= 5, то при умножении на (x-3) знак неравенства остается
Решаем точно такой же заменой.
y^2 + y - 6 < 0
(y + 3)(y - 2) < 0
y ∈ (-3; 2), но y >= 0, поэтому
y ∈ [0; 2)
{
{
x^2 - 8x + 15 < 4
x^2 - 8x + 11 < 0
D/4 = 4^2 - 11 = 16 - 11 = 5
x1 = 4 - √5 ~ 1,764 < 5
x2 = 4 + √5 ~ 6,236 > 5
x ∈ (4-√5; 4+√5), но x >= 5, поэтому
x ∈ [5; 4+√5) - ЭТО РЕШЕНИЕ.
Ответ: (-oo; 4-√5) U [5; 4+√5)
Удачник66:
А что вам не нравится? Или вы хотите сказать, что 0 > 3 ?
Да, понял,, в чем ошибка. Извиняюсь за наезд.
Я всегда стараюсь свести уравнение к квадратному. А у вас способ вообще другой.
Спасибо, большое!!!)))
Похожие вопросы
Предмет: Английский язык,
автор: kirsall
Предмет: Математика,
автор: nelasistaluk
Предмет: Биология,
автор: Аноним
Предмет: Русский язык,
автор: NiggaSdogga3
Предмет: Английский язык,
автор: asyasarsenova83