Question

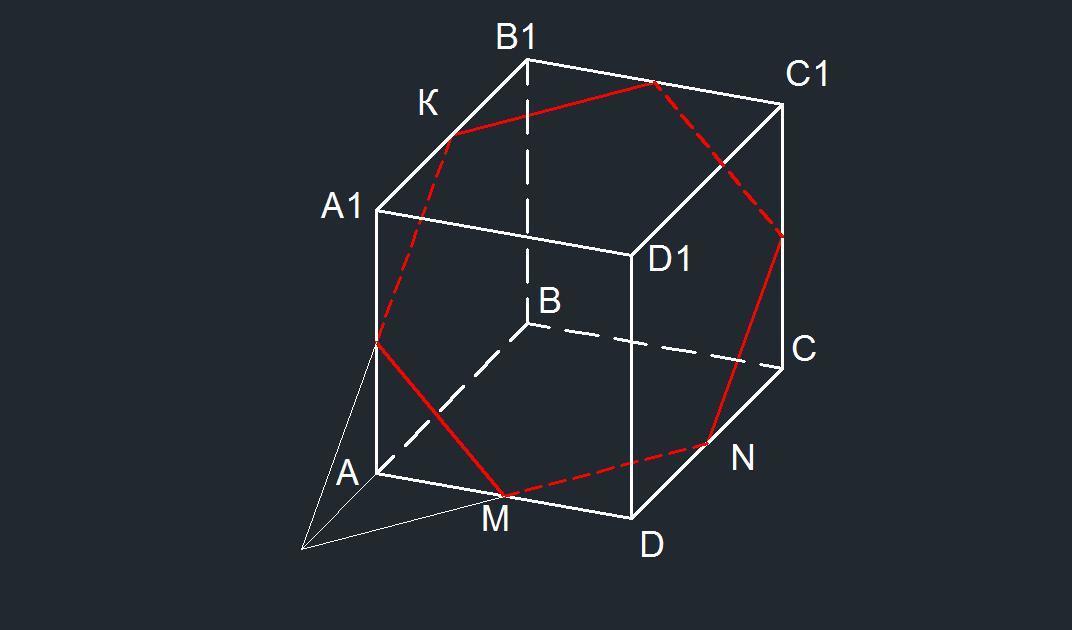
В правильной четырехугольной призме АВСDА1B1C1D1 стороны основания ABCD равны 4, а боковые ребра AA1, BB1, CC1 равны 6. Найдите площадь сечения призмы проходящего через середины ребер AB, AD, B1C1.

Answer 1

В сечении имеем шестиугольник.
Две стороны сечения призмы, проходящего через середины ребер AB, AD, B1C1, это отрезки длиной 2√2.
Боковые стороны равны √(2²+3²) =√(4+9) = √13.
Наклонная длина шестиугольника равна L = √(6²+(2√2)²) = √(36+8) = √44 = 2√11.
Ширина его по диагонали, параллельной основаниям, равна диагонали основания призмы В = 4√2.
Сечение состоит из двух трапеций с равными основаниями.
S = Вср*L = ((2√2+4√2)/2)*2√11 = 3√2*2√11 = 6√22 кв.ед.