Предмет: Математика,
автор: Аноним
Интересный пример 124))))
Решить уравнение: ![\sqrt[5]{ \dfrac{1}{2} -\sin x} + \sqrt[5 ]{ \dfrac{1}{2}+\sin x} =1 \sqrt[5]{ \dfrac{1}{2} -\sin x} + \sqrt[5 ]{ \dfrac{1}{2}+\sin x} =1](https://tex.z-dn.net/?f=+%5Csqrt%5B5%5D%7B+%5Cdfrac%7B1%7D%7B2%7D+-%5Csin+x%7D+%2B+%5Csqrt%5B5+%5D%7B+%5Cdfrac%7B1%7D%7B2%7D%2B%5Csin+x%7D+%3D1)
Ответы
Автор ответа:
3
Решение на фотографиях. Ответы можно как-то объединить, по идее.
Приложения:
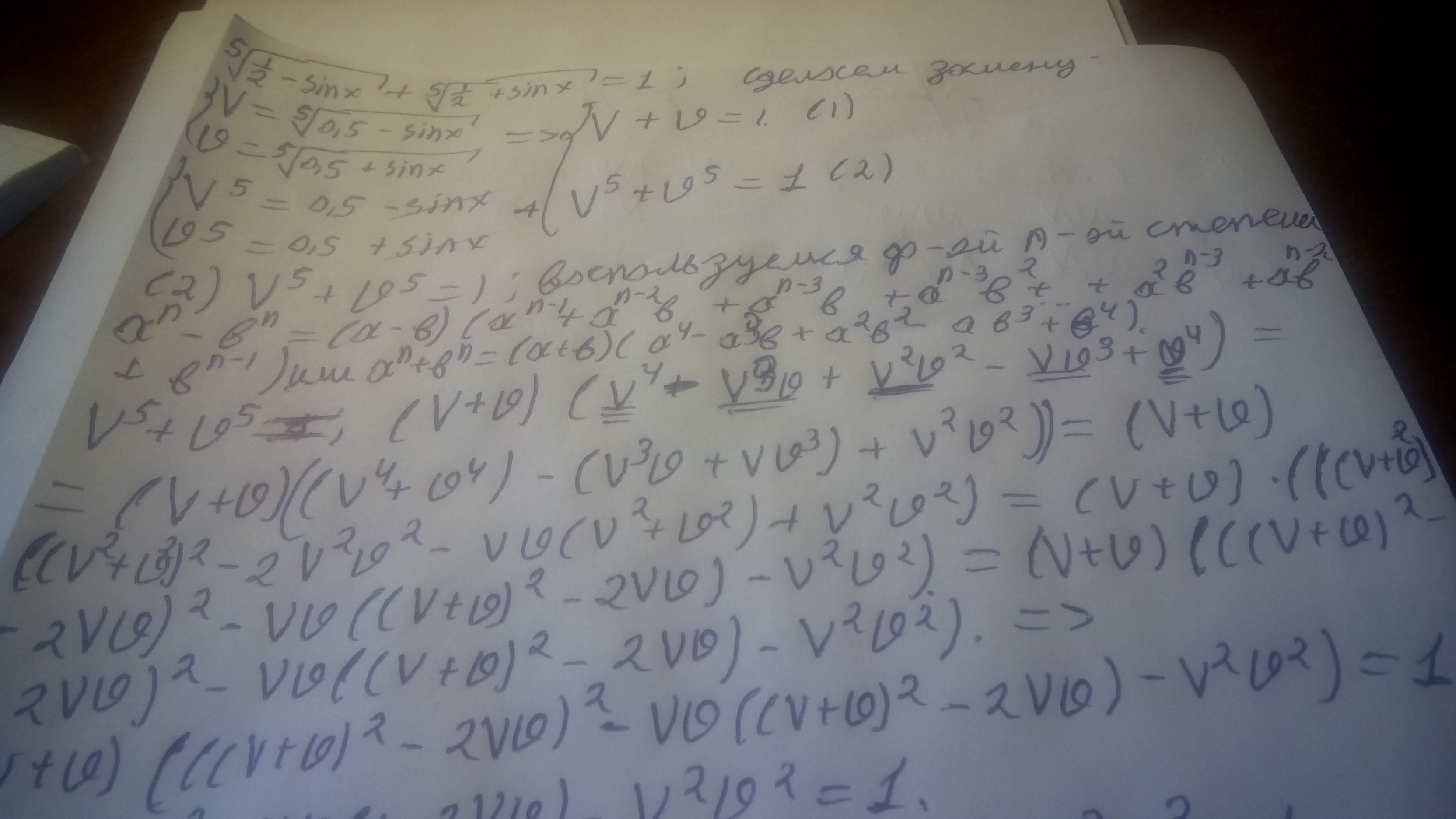


Автор ответа:
2
Для тех, кто не любит приложенные файлы, повторю решение.
![\sqrt[5]{ \frac{1}{2} -sin(x)} =a; \sqrt[5]{ \frac{1}{2} +sin(x)} =b \sqrt[5]{ \frac{1}{2} -sin(x)} =a; \sqrt[5]{ \frac{1}{2} +sin(x)} =b](https://tex.z-dn.net/?f=+%5Csqrt%5B5%5D%7B+%5Cfrac%7B1%7D%7B2%7D+-sin%28x%29%7D+%3Da%3B++%5Csqrt%5B5%5D%7B+%5Cfrac%7B1%7D%7B2%7D+%2Bsin%28x%29%7D+%3Db)
{ a + b = 1
{ a^5 + b^5 = (1/2 - sin x) + (1/2 + sin x) = 1
Раскладываем a^5 + b^5 на множители
a^5 + b^5 = (a+b)(a^4 - a^3*b + a^2*b^2 - a*b^3 + b^4)
Подставляем данные из системы
1 = 1(a^4 - a^3*b + a^2*b^2 - a*b^3 + b^4)
Записываем в более привычном виде
(a^4 + b^4 + a^2*b^2 ) - (a^3*b + a*b^3) = 1
Выделяем полные квадраты
(a^4 + 2a^2*b^2 + b^4 - a^2*b^2) - ab*(a^2 + b^2) = 1
Сворачиваем в квадраты
(a^2 + b^2)^2 - a^2*b^2 - ab*(a^2 + b^2) = 1
Опять выделяем полные квадраты
(a^2 + 2ab + b^2 - 2ab)^2 - ab*(a^2 + 2ab + b^2 - 2ab) - a^2*b^2 = 1
Опять сворачиваем в квадраты
( (a+b)^2 - 2ab)^2 - ab( (a+b)^2 - 2ab) - a^2*b^2 = 1
Подставляем a+b = 1, отсюда (a+b)^2 = 1
(1 - 2ab)^2 - ab(1 - 2ab) - a^2*b^2 = 1
Раскрываем скобки
1 - 4ab + 4a^2*b^2 - ab + 2a^2*b^2 - a^2*b^2 = 1
Приводим подобные
-5ab + 5a^2*b^2 = 0
5ab(ab - 1) = 0
Решения:
1)![a= \sqrt[5]{ \frac{1}{2} -sin(x)} =0 a= \sqrt[5]{ \frac{1}{2} -sin(x)} =0](https://tex.z-dn.net/?f=a%3D+%5Csqrt%5B5%5D%7B+%5Cfrac%7B1%7D%7B2%7D+-sin%28x%29%7D+%3D0)
1/2 - sin x = 0
sin x = 1/2
x1 = pi/6 + 2pi*k; x2 = 5pi/6 + 2pi*k
2)![b= \sqrt[5]{ \frac{1}{2} +sin(x)} =0 b= \sqrt[5]{ \frac{1}{2} +sin(x)} =0](https://tex.z-dn.net/?f=b%3D+%5Csqrt%5B5%5D%7B+%5Cfrac%7B1%7D%7B2%7D+%2Bsin%28x%29%7D+%3D0)
sin x = -1/2
x3 = -pi/6 + 2pi*k; x4 = -5pi/6 + 2pi*k
3)![ab= \sqrt[5]{ \frac{1}{2} -sin(x)}*\sqrt[5]{ \frac{1}{2} +sin(x)}=\sqrt[5]{ \frac{1}{4} -sin^2(x)}=1 ab= \sqrt[5]{ \frac{1}{2} -sin(x)}*\sqrt[5]{ \frac{1}{2} +sin(x)}=\sqrt[5]{ \frac{1}{4} -sin^2(x)}=1](https://tex.z-dn.net/?f=ab%3D+%5Csqrt%5B5%5D%7B+%5Cfrac%7B1%7D%7B2%7D+-sin%28x%29%7D%2A%5Csqrt%5B5%5D%7B+%5Cfrac%7B1%7D%7B2%7D+%2Bsin%28x%29%7D%3D%5Csqrt%5B5%5D%7B+%5Cfrac%7B1%7D%7B4%7D+-sin%5E2%28x%29%7D%3D1)
1/4 - sin^2 x = 1
sin^2 x = 1/4 - 1 = -3/4 < 0
Корней нет.
Ответ: x1 = pi/6 + 2pi*k; x2 = 5pi/6 + 2pi*k
x3 = -pi/6 + 2pi*k; x4 = -5pi/6 + 2pi*k
{ a + b = 1
{ a^5 + b^5 = (1/2 - sin x) + (1/2 + sin x) = 1
Раскладываем a^5 + b^5 на множители
a^5 + b^5 = (a+b)(a^4 - a^3*b + a^2*b^2 - a*b^3 + b^4)
Подставляем данные из системы
1 = 1(a^4 - a^3*b + a^2*b^2 - a*b^3 + b^4)
Записываем в более привычном виде
(a^4 + b^4 + a^2*b^2 ) - (a^3*b + a*b^3) = 1
Выделяем полные квадраты
(a^4 + 2a^2*b^2 + b^4 - a^2*b^2) - ab*(a^2 + b^2) = 1
Сворачиваем в квадраты
(a^2 + b^2)^2 - a^2*b^2 - ab*(a^2 + b^2) = 1
Опять выделяем полные квадраты
(a^2 + 2ab + b^2 - 2ab)^2 - ab*(a^2 + 2ab + b^2 - 2ab) - a^2*b^2 = 1
Опять сворачиваем в квадраты
( (a+b)^2 - 2ab)^2 - ab( (a+b)^2 - 2ab) - a^2*b^2 = 1
Подставляем a+b = 1, отсюда (a+b)^2 = 1
(1 - 2ab)^2 - ab(1 - 2ab) - a^2*b^2 = 1
Раскрываем скобки
1 - 4ab + 4a^2*b^2 - ab + 2a^2*b^2 - a^2*b^2 = 1
Приводим подобные
-5ab + 5a^2*b^2 = 0
5ab(ab - 1) = 0
Решения:
1)
1/2 - sin x = 0
sin x = 1/2
x1 = pi/6 + 2pi*k; x2 = 5pi/6 + 2pi*k
2)
sin x = -1/2
x3 = -pi/6 + 2pi*k; x4 = -5pi/6 + 2pi*k
3)
1/4 - sin^2 x = 1
sin^2 x = 1/4 - 1 = -3/4 < 0
Корней нет.
Ответ: x1 = pi/6 + 2pi*k; x2 = 5pi/6 + 2pi*k
x3 = -pi/6 + 2pi*k; x4 = -5pi/6 + 2pi*k
Похожие вопросы
Предмет: Геометрия,
автор: koro4evarya
Предмет: Литература,
автор: nytichekruban
Предмет: Английский язык,
автор: stanyves
Предмет: Обществознание,
автор: Yusuf26
Предмет: Биология,
автор: aminat20017