Предмет: Алгебра,
автор: Djavidan26
Срочно пожалуйста решите 533 и 534.Даю 20 баллов.Срочно надо!!!
Приложения:
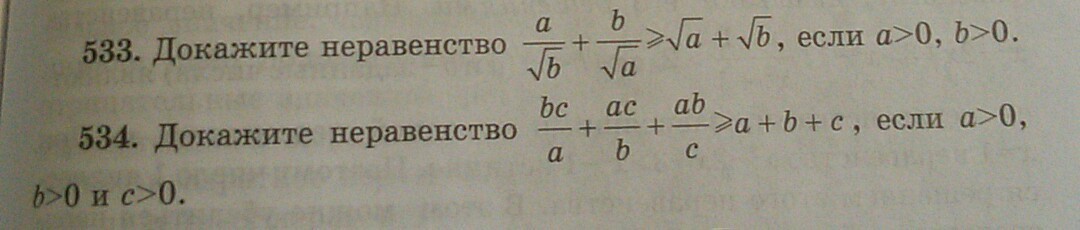
Аноним:
Какой класс?
8 класс
Автор какой ещё?
шыныбеков
Ответы
Автор ответа:
0
533) 


Нам надо это доказать. Докажем, что

Умножим все на √(ab)
a - √(ab) + b >= √(ab)
a + b >= 2√(ab)
(a + b)/2 >= √(ab)
Это очевидно, среднее арифметическое двух чисел всегда больше или равно среднего геометрического.
Равно - если числа равны, то есть при a = b.
534)

Дальше не знаю
Нам надо это доказать. Докажем, что
Умножим все на √(ab)
a - √(ab) + b >= √(ab)
a + b >= 2√(ab)
(a + b)/2 >= √(ab)
Это очевидно, среднее арифметическое двух чисел всегда больше или равно среднего геометрического.
Равно - если числа равны, то есть при a = b.
534)
Дальше не знаю
Похожие вопросы
Предмет: Литература,
автор: sonikovganich
Предмет: Химия,
автор: Anastasiya1357378
Предмет: Геометрия,
автор: silveeeer
Предмет: Математика,
автор: violetta852
Предмет: Математика,
автор: 18081989