Предмет: Математика,
автор: Kandrael
Решить уравнение и в ответ записать сумму решений, принадлежащих отрезку [0; ]
]
Приложения:
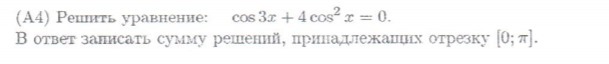
Ответы
Автор ответа:
0
Произведение равно нулю, если один из множителей равен нулю
пусть
Обратная замена
Отбор корней на отрезке [0;π].
Для корня
Для корня
Для корня
Сумма решений на отрезке [0;π]:
Ответ:
Похожие вопросы
Предмет: Алгебра,
автор: yasyanagorna
Предмет: Английский язык,
автор: livesale063
Предмет: Математика,
автор: xjxkdjskxkxk
Предмет: Математика,
автор: Аноним
Предмет: Физкультура и спорт,
автор: danilca516