Предмет: Геометрия,
автор: popopolli
Вычислить площадь равнобедренного треугольника , если прямая, соединяющая середины основания и боковой стороны равна половине радиуса R описанного круга
Приложения:
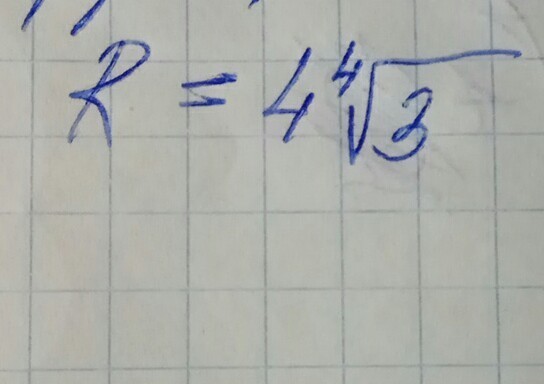
nabludatel00:
либо я отупел, либо что-то не понимаю.... Проверьте условие, а то у меня абсурд получается..
Ответы
Автор ответа:
4
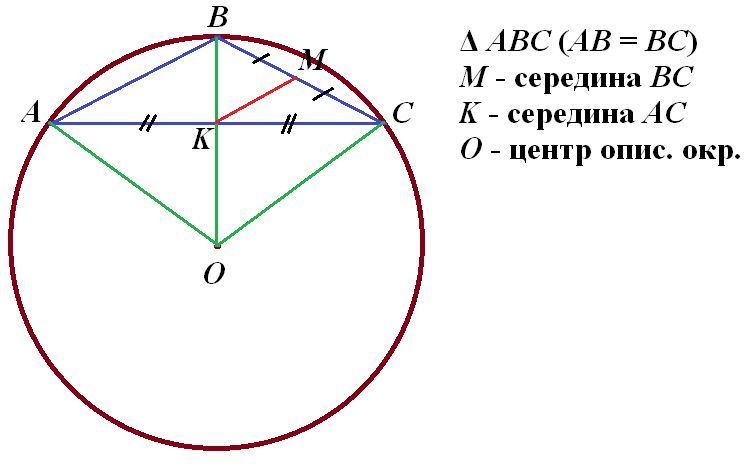
Чертеж во вложении.
Рассмотрим равнобедренный ΔАВС (АВ=ВС). Пусть М-середина ВС, К - середина АС. Тогда КМ - средняя линия ΔАВС, которая по условию равна радиусу R описанной окружности. Тогда по свойству средней линии треугольника АВ = 2КМ = R = BC. Отсюда следует вывод, если боковая сторона равнобедренного треугольника равна радиусу описанной около него окружности, то такой треугольник - тупоугольный.
Используя теорему синусов для ΔАВС, получим соотношение:
 , отсюда
, отсюда


По условию![R=4 \sqrt[4]{3} R=4 \sqrt[4]{3}](https://tex.z-dn.net/?f=R%3D4+%5Csqrt%5B4%5D%7B3%7D+) . Тогда
. Тогда
![S_{ABC}= \dfrac{(4 \sqrt[4]{3} )^2*\sqrt3}{4} =4*3=12 S_{ABC}= \dfrac{(4 \sqrt[4]{3} )^2*\sqrt3}{4} =4*3=12](https://tex.z-dn.net/?f=S_%7BABC%7D%3D++%5Cdfrac%7B%284+%5Csqrt%5B4%5D%7B3%7D+%29%5E2%2A%5Csqrt3%7D%7B4%7D+%3D4%2A3%3D12)
Ответ: 12.
Рассмотрим равнобедренный ΔАВС (АВ=ВС). Пусть М-середина ВС, К - середина АС. Тогда КМ - средняя линия ΔАВС, которая по условию равна радиусу R описанной окружности. Тогда по свойству средней линии треугольника АВ = 2КМ = R = BC. Отсюда следует вывод, если боковая сторона равнобедренного треугольника равна радиусу описанной около него окружности, то такой треугольник - тупоугольный.
Используя теорему синусов для ΔАВС, получим соотношение:
По условию
Ответ: 12.
Приложения:
100%! а я рисунок не тот сделал...
Автор ответа:
4
Хочу предложить решение данной задачи через рассмотрение полученного в ходе решения равностороннего треугольника.
Приложения:

Похожие вопросы
Предмет: Геометрия,
автор: viktoriaursta5
Предмет: Английский язык,
автор: Anastasia5223
Предмет: Математика,
автор: Iriwiwik
Предмет: История,
автор: EnergyTop
Предмет: История,
автор: mashai2018