Предмет: Математика,
автор: popopolli
Помогите решить уравнение, пожалуйста
Приложения:
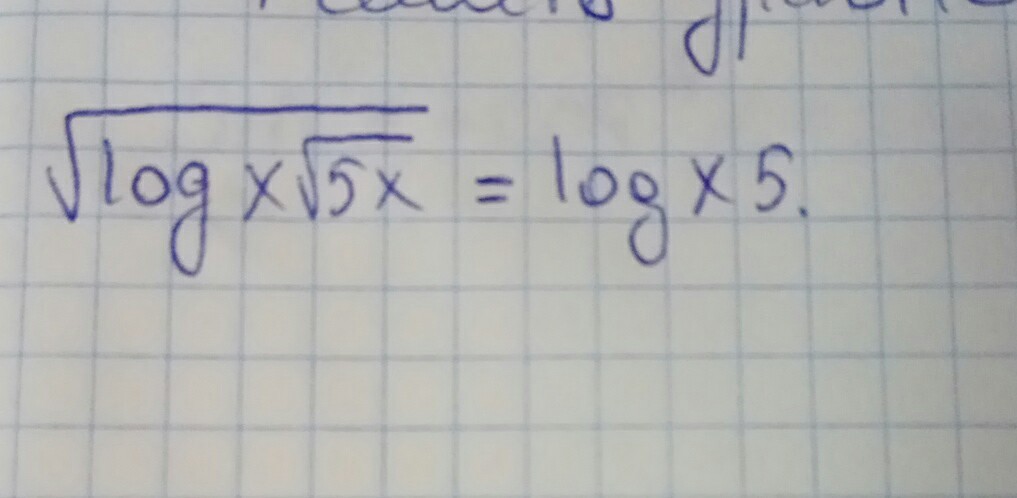
Ответы
Автор ответа:
1
ОДЗ:


(1)/////////////>x
(0,2)///////////////////////////////>x
(0)///////////////////////(1) >x
//////////////(0,2)


(1)/////////////>x
////////////////////////////////////////////////////>x
(0)///////////////////////(1) >x
>x

В общем получаем ОДЗ: x>1


Ответ: х=5
(1)/////////////>x
(0,2)///////////////////////////////>x
(0)///////////////////////(1) >x
//////////////(0,2)
(1)/////////////>x
////////////////////////////////////////////////////>x
(0)///////////////////////(1) >x
>x
В общем получаем ОДЗ: x>1
Ответ: х=5
Похожие вопросы
Предмет: Геометрия,
автор: pochta7390
Предмет: Физкультура и спорт,
автор: ZmeecapkaKV
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: vintket
Предмет: Алгебра,
автор: ftfdrdsee