Предмет: Геометрия,
автор: AldiyarAmanbaev
Помогите решить ребят:В треугольнике ABC сторона AB=3, высота , опущенная на сторону AB , равна 3. Основание D высоты CD лежит на стороне AB, длина отрезка AD равна длине стороны BC . Найти длину стороны AC .
cos20093:
По условию AD < AB и CD < BC; это противоречит тому, что AB = CD и AD = BC;
спасибо
я и не учел этого
хотя в задаче так написано
значит, задача неправильная
вернее, она правильная, но...
Ответы
Автор ответа:
2
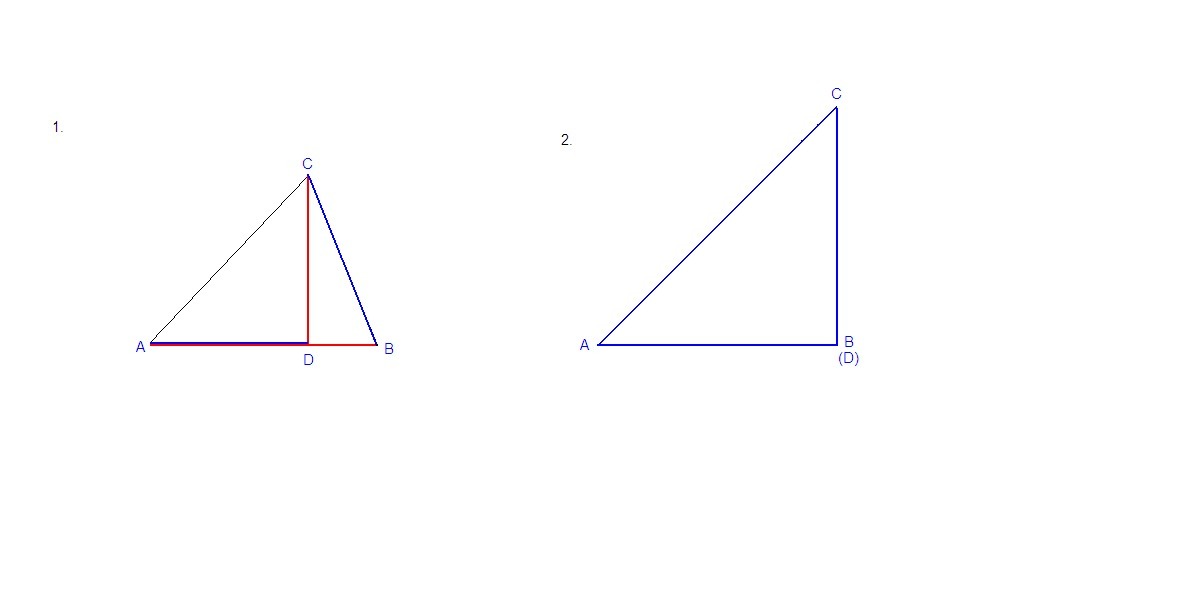
1. Пусть точка D не совпадает с концами отрезка АВ (рис. 1).
Тогда AD < AB, AD < 3,
а ВС > СD, BC > 3 так как в прямоугольном треугольнике BCD гипотенуза BC больше катета.
Итак, AD < 3, а BC > 3, а по условию AD = BC, значит такое расположение точки D невозможно.
2. Точка D не может совпадать с точкой А, так как тогда длина отрезка AD = 0, и ВС = AD = 0.
3. Значит точка D совпадает с точкой В. В таком случае ΔАВС прямоугольный, равнобедренный.
По теореме Пифагора:
АС = √(АВ² + ВС²) = √(9 + 9) = √18 = 9√2
Приложения:
Похожие вопросы
Предмет: Немецкий язык,
автор: yourheeell
Предмет: Алгебра,
автор: paraschynsofia
Предмет: Українська мова,
автор: davidkapysta
Предмет: Обществознание,
автор: valeriah2009
Предмет: История,
автор: zunaruvvvvv