Предмет: Геометрия,
автор: Teaminxl
ПОМОГИТЕ ПОЖАЛУЙСТА!!!!
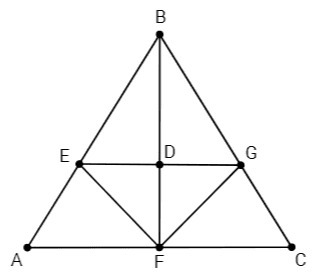
В равнобедренный треугольник ABC (AB=BC) вписан равнобедренный прямоугольный треугольник так, что вершина прямого угла лежит на основании данного треугольника, а гипотенуза параллельна основанию (вершины острых углов лежат на боковых сторонах треугольника).
Найдите площадь прямоугольного треугольника, если высота BF=16, а AB=20.
Ответы
Автор ответа:
3
По теореме Пифагора:
AF= √(AB^2-BF^2) = √(20^2-16^2) =12
ABF~EBD (∠BAF=∠BED, ∠BFA=∠BDE как соответственные при AF||ED)
ED/BD=AF/BF =12/16=3/4
ED=DF (высота в равнобедренном треугольнике является медианой; медиана в прямоугольном треугольнике равна половине гипотенузы).
BD=BF-DF=16-DF
DF/(16-DF)=3/4 <=> DF=48/7 (~6,86)
EG=2DF
SEGF= EG*DF/2 = DF^2 =(48/7)^2 = 47 1/49 (~47,02)
AF= √(AB^2-BF^2) = √(20^2-16^2) =12
ABF~EBD (∠BAF=∠BED, ∠BFA=∠BDE как соответственные при AF||ED)
ED/BD=AF/BF =12/16=3/4
ED=DF (высота в равнобедренном треугольнике является медианой; медиана в прямоугольном треугольнике равна половине гипотенузы).
BD=BF-DF=16-DF
DF/(16-DF)=3/4 <=> DF=48/7 (~6,86)
EG=2DF
SEGF= EG*DF/2 = DF^2 =(48/7)^2 = 47 1/49 (~47,02)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: olgabilokon05
Предмет: Геометрия,
автор: maksfedoruk3
Предмет: Информатика,
автор: tacenkonazar6
Предмет: Математика,
автор: abibulla123
Предмет: Русский язык,
автор: ShishkaLub