Предмет: Математика,
автор: RedOwl99
Помогите решить олимпиаду (5)
Приложения:
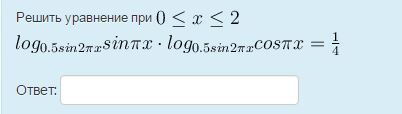
Ответы
Автор ответа:
1
Недавно решал эту задачу.
0,5*sin(2pi*x) = 0,5*2sin(pi*x)*cos(pi*x) = sin(pi*x)*cos(pi*x)

У логарифмов есть такое свойство:

Причем новое основание c может быть каким угодно, например, 10.

Логарифм произведения равен сумме логарифмов

![\frac{lg(sin( \pi x))*lg(cos( \pi x))}{[lg(sin( \pi x))+lg(cos( \pi x))]^2} = \frac{1}{4} \frac{lg(sin( \pi x))*lg(cos( \pi x))}{[lg(sin( \pi x))+lg(cos( \pi x))]^2} = \frac{1}{4}](https://tex.z-dn.net/?f=+%5Cfrac%7Blg%28sin%28+%5Cpi+x%29%29%2Alg%28cos%28+%5Cpi+x%29%29%7D%7B%5Blg%28sin%28+%5Cpi+x%29%29%2Blg%28cos%28+%5Cpi+x%29%29%5D%5E2%7D+%3D+%5Cfrac%7B1%7D%7B4%7D+)
4lg(sin(pi*x))*lg(cos(pi*x)) = [ lg(sin(pi*x)) + lg(cos(pi*x)) ]^2
4lg(sin(pix))*lg(cos(pix)) = lg^2(sin(pix)) + 2lg(sin(pix))*lg(cos(pix)) + lg^2(cos(pix))
lg^2(sin(pix)) - 2lg(sin(pix))*lg(cos(pix)) + lg^2(cos(pix)) = 0
[ lg(sin(pi*x)) - lg(cos(pi*x)) ]^2 = 0
lg(sin(pi*x)) = lg(cos(pi*x))
Если равны логарифмы по одинаковому основанию, то равны и числа под логарифмами
sin(pi*x) = cos(pi*x)
tg(pi*x) = 1
pi*x = pi/4 + pi*k
Если x ∈ [0; 2], то корней всего два:
x1 = 1/4; x2 = 5/4
Однако, при x=5pi/4 будет sin(pi*x)=sin(5pi/4)=-1/√2<0; cos(5pi/4)=-1/√2<0
Эти числа не могут стоять под логарифмом. Поэтому
Ответ: x = 1/4
0,5*sin(2pi*x) = 0,5*2sin(pi*x)*cos(pi*x) = sin(pi*x)*cos(pi*x)
У логарифмов есть такое свойство:
Причем новое основание c может быть каким угодно, например, 10.
Логарифм произведения равен сумме логарифмов
4lg(sin(pi*x))*lg(cos(pi*x)) = [ lg(sin(pi*x)) + lg(cos(pi*x)) ]^2
4lg(sin(pix))*lg(cos(pix)) = lg^2(sin(pix)) + 2lg(sin(pix))*lg(cos(pix)) + lg^2(cos(pix))
lg^2(sin(pix)) - 2lg(sin(pix))*lg(cos(pix)) + lg^2(cos(pix)) = 0
[ lg(sin(pi*x)) - lg(cos(pi*x)) ]^2 = 0
lg(sin(pi*x)) = lg(cos(pi*x))
Если равны логарифмы по одинаковому основанию, то равны и числа под логарифмами
sin(pi*x) = cos(pi*x)
tg(pi*x) = 1
pi*x = pi/4 + pi*k
Если x ∈ [0; 2], то корней всего два:
x1 = 1/4; x2 = 5/4
Однако, при x=5pi/4 будет sin(pi*x)=sin(5pi/4)=-1/√2<0; cos(5pi/4)=-1/√2<0
Эти числа не могут стоять под логарифмом. Поэтому
Ответ: x = 1/4
RedOwl99:
Огромное спасибо!
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: danillllaghgh
Предмет: История,
автор: sophiaivanova120710
Предмет: География,
автор: tagirova0115
Предмет: Математика,
автор: Аноним