Предмет: Геометрия,
автор: Teaminxl
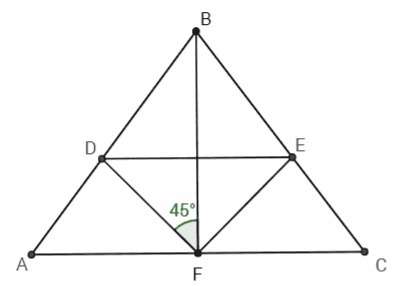
В равнобедренный треугольник ABC (AB=BC) вписан равнобедренный прямоугольный треугольник так, что вершина прямого угла лежит на основании данного треугольника, а гипотенуза параллельна основанию (вершины острых углов лежат на боковых сторонах треугольника).
Найдите площадь прямоугольного треугольника, если высота BF=16, а AB=20.
Ответы
Автор ответа:
3
cos(ABF)= BF/AB = 16/20 =0,8
∠DBF = arccos(0,8) =36,86
∠FDB= 180 -∠BFD -∠DBF = 180 -45 -36,86 =98,14
DF= BF*sin(DBF)/sin(FDB) = 16*sin(36,86)/sin(98,14) =9,69
S FDE= FD^2/2 = 9,69^2 =46,99
∠DBF = arccos(0,8) =36,86
∠FDB= 180 -∠BFD -∠DBF = 180 -45 -36,86 =98,14
DF= BF*sin(DBF)/sin(FDB) = 16*sin(36,86)/sin(98,14) =9,69
S FDE= FD^2/2 = 9,69^2 =46,99
Приложения:
Похожие вопросы
Предмет: Биология,
автор: oGGffrrghb
Предмет: Алгебра,
автор: dragneelvasa
Предмет: Литература,
автор: zharovaariana83
Предмет: Алгебра,
автор: НяшаНет
Предмет: Українська мова,
автор: xoklig