Предмет: Алгебра,
автор: Tomkaya
Помогите с решением, пожалуйста
Приложения:
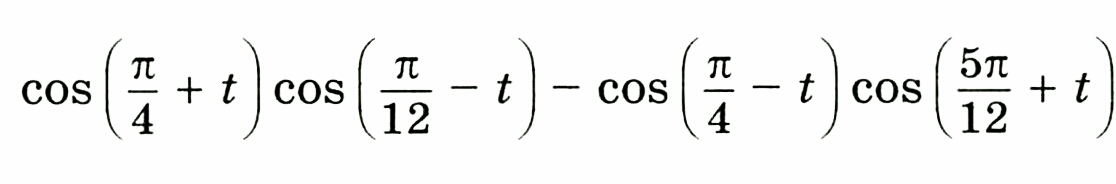
Ответы
Автор ответа:
0
1/2 ×(сos(п/6+2t)+cos(п/3))-1/2 ×(cos(-п/6-2t)+cos(2п/3))=1/2 ×(сos(п/6+2t)+1/2)-1/2 ×(cos(п/6+2t)-1/2)=1/2 ×сos(п/6+2t) +1/4 -1/2 ×cos(п/6+2t) +1/4=1/2
Автор ответа:
1
cos(π/4-t)=cos(π/2-(π/4+t))=sin(π/4+t)
cos(5π/12+t)=cos(π/2-(π/12-t))=sin(π/12-t)
------------------------------
cos(π/4+t)cos(π/12-t)-sin(π/4+t)sin(π/12-t)=cos(π/4+t+π/12-t)=
=cosπ/3=1/2
cos(5π/12+t)=cos(π/2-(π/12-t))=sin(π/12-t)
------------------------------
cos(π/4+t)cos(π/12-t)-sin(π/4+t)sin(π/12-t)=cos(π/4+t+π/12-t)=
=cosπ/3=1/2
Похожие вопросы
Предмет: Математика,
автор: novikovamargarita324
Предмет: Физика,
автор: ghjmord
Предмет: География,
автор: vladdorosuk09
Предмет: Английский язык,
автор: pofigunetima
Предмет: Физика,
автор: Rhi6