Предмет: Математика,
автор: FlameInBrain
Помогите решить интеграл
Приложения:
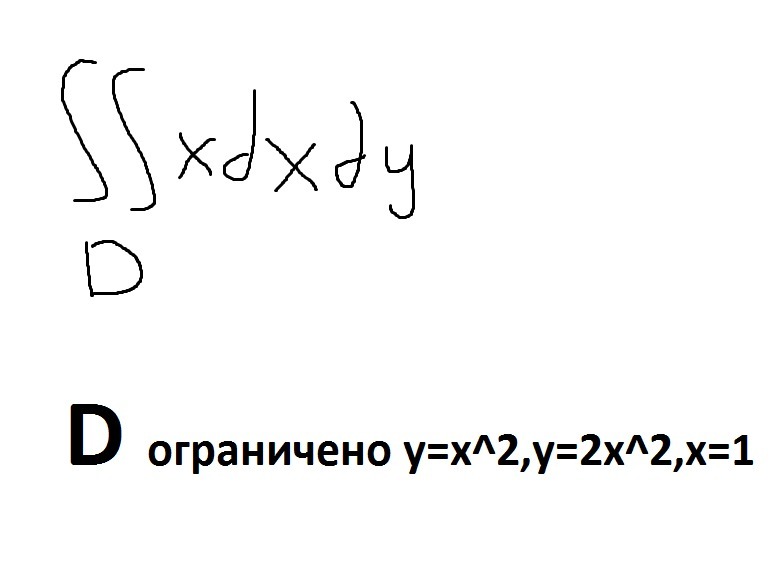
Ответы
Автор ответа:
0
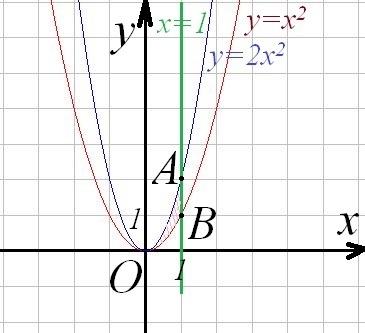
Строим область D (на рисунке во вложении).
По рисунку видим, что при изменении параметра х от 0 до 1 параметр у меняется от линии до линии
до линии  . Получим пределы интегрирования для повторного интеграла.
. Получим пределы интегрирования для повторного интеграла.
Таким образом,

По рисунку видим, что при изменении параметра х от 0 до 1 параметр у меняется от линии
Таким образом,
Приложения:
Похожие вопросы
Предмет: История,
автор: zdotapo
Предмет: Математика,
автор: m99880363
Предмет: Физика,
автор: Аноним
Предмет: Литература,
автор: detylotova