Предмет: Математика,
автор: FlameInBrain
Помогите решить интеграл
Приложения:
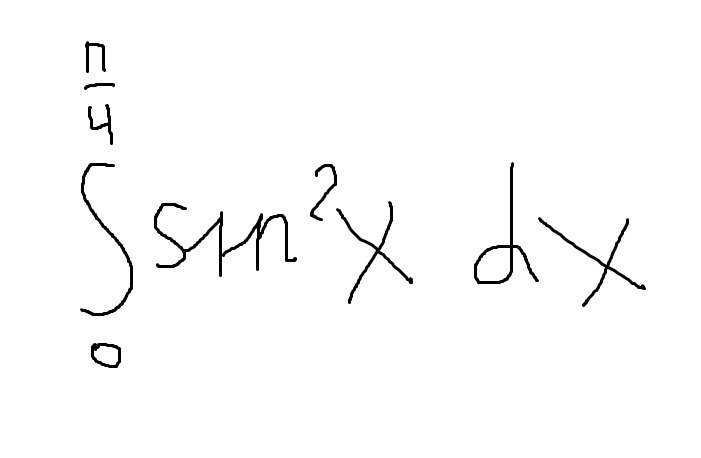
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Окружающий мир,
автор: oliviadenizonel
Предмет: Другие предметы,
автор: bekalex1209
Предмет: Қазақ тiлi,
автор: isimovsayan002
Предмет: Математика,
автор: Sofia21032012
Предмет: Математика,
автор: Аноним