Предмет: Алгебра,
автор: Basto2
Решите неравенство:
Приложения:
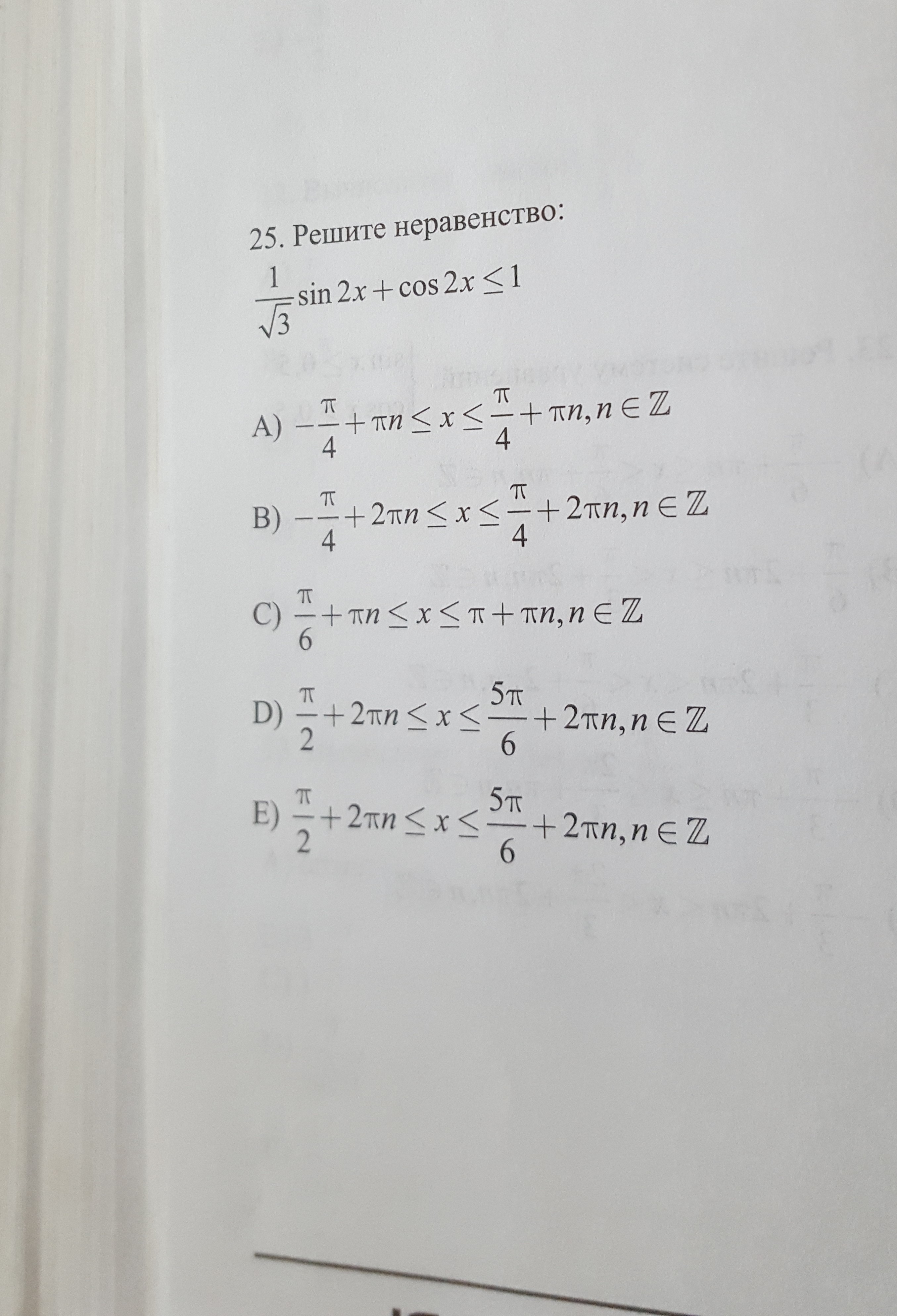
Ответы
Автор ответа:
1
Умножаем все на √3
sin 2x + √3*cos 2x <= √3
2sin x*cos x + √3cos^2 x - √3*sin^2 x <= √3*cos^2 x + √3*sin^2 x
2sin x*cos x - 2√3*sin^2 x <= 0
2sin x*(cos x - √3*sin x) <= 0
1) sin x = 0; x1 = pi*n
2) √3*sin x = cos x
tg x = 1/√3; x2 = pi/6 + pi*n
Ответ: С) pi/6 + pi*n <= x <= pi + pi*n
sin 2x + √3*cos 2x <= √3
2sin x*cos x + √3cos^2 x - √3*sin^2 x <= √3*cos^2 x + √3*sin^2 x
2sin x*cos x - 2√3*sin^2 x <= 0
2sin x*(cos x - √3*sin x) <= 0
1) sin x = 0; x1 = pi*n
2) √3*sin x = cos x
tg x = 1/√3; x2 = pi/6 + pi*n
Ответ: С) pi/6 + pi*n <= x <= pi + pi*n
Похожие вопросы
Предмет: Информатика,
автор: elenakaramella
Предмет: Қазақ тiлi,
автор: astutor94
Предмет: Математика,
автор: danielsulanov
Предмет: Химия,
автор: shudiana111
Предмет: Алгебра,
автор: cats0up