Предмет: Геометрия,
автор: Ryana22222222
Помогите пожалуйста!очень нужно!!
Прямоугольные треугольники,их элементы.Формулировка теоремы Пифагора.
Ответы
Автор ответа:
4
Элементы любого треугольника (в том числе и прямоугольного): высота, биссектриса, медиана, срединный перпендикуляр.
Элементы прямоугольного треугольника: прямой угол, два острых угла, гипотенуза (самая длинная сторона, лежит против прямого угла), катеты (лежат против острых углов).
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов; a²=b²+c²
Элементы прямоугольного треугольника: прямой угол, два острых угла, гипотенуза (самая длинная сторона, лежит против прямого угла), катеты (лежат против острых углов).
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов; a²=b²+c²
Ryana22222222:
Спасибо!
Автор ответа:
4
Прямоугольный треугольник - это треугольник в котором один из углов прямой, т.е. равен 90°
Две стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла называется гипотенуза. Причем гипотенуза всегда больше любого из катетов.
Свойства прямоугольного треугольника:
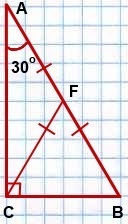
1. Катет, лежажий против угла в 30° равен половине гипотенузы.
2. Медиана, проведенная к гипотенузе, равна половине гипотенузы.
3. Сумма двух острых углов прямоугольного треугольника равна 90°
Признаки равенства прямоугольных треугольников:
1. По двум катетам (Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны)
2. По катету и гипотенузе (Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны)
3. По катету и острому углу (Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны)
4. По гипотенузе и острому углу (Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны)
Площадь прямоугольного треугольника равна половине произведения его катетов.
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема, обратная теореме Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
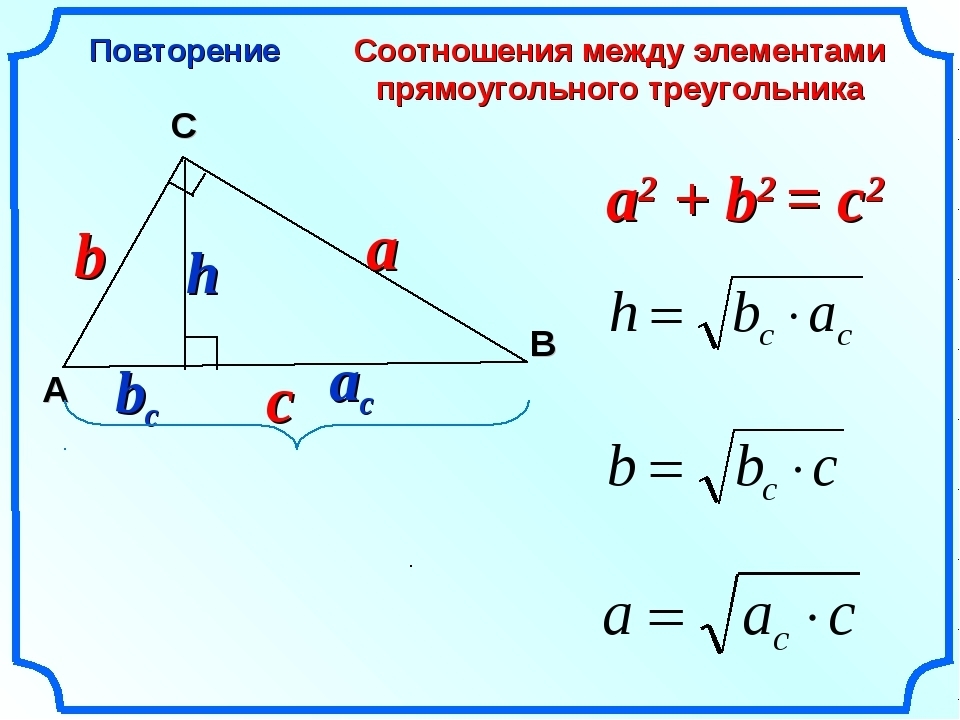
P.S. говоря об элементах треугольника в 8 классе учителя математики часто задают заполнить таблицу, где присутствуют такие элементы прямоугольного треугольника как a-катет, b-катет, c-гипотенуза, h-высота , и
и  -проекции катетов на гипотенузу. Формулы их нахождения и рисунок прилагаю в виде картинки.
-проекции катетов на гипотенузу. Формулы их нахождения и рисунок прилагаю в виде картинки.
Две стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла называется гипотенуза. Причем гипотенуза всегда больше любого из катетов.
Свойства прямоугольного треугольника:
1. Катет, лежажий против угла в 30° равен половине гипотенузы.
2. Медиана, проведенная к гипотенузе, равна половине гипотенузы.
3. Сумма двух острых углов прямоугольного треугольника равна 90°
Признаки равенства прямоугольных треугольников:
1. По двум катетам (Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны)
2. По катету и гипотенузе (Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны)
3. По катету и острому углу (Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны)
4. По гипотенузе и острому углу (Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны)
Площадь прямоугольного треугольника равна половине произведения его катетов.
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема, обратная теореме Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
P.S. говоря об элементах треугольника в 8 классе учителя математики часто задают заполнить таблицу, где присутствуют такие элементы прямоугольного треугольника как a-катет, b-катет, c-гипотенуза, h-высота ,
Приложения:

Спасибо огромное!
Добавила немножко про проекции катетов.
Не за что! Надеюсь помогла
Похожие вопросы
Предмет: Қазақ тiлi,
автор: cina09053
Предмет: Информатика,
автор: deti48519
Предмет: Математика,
автор: ekaterina8247
Предмет: Алгебра,
автор: redir626
Предмет: Алгебра,
автор: vladprihodkodon