Предмет: Алгебра,
автор: Longnoses
Помогите пожалуйста решить
Приложения:
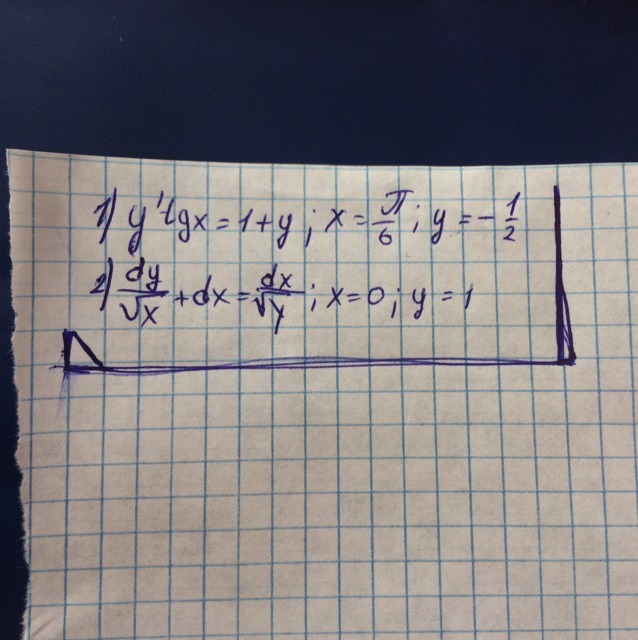
Ответы
Автор ответа:
0
Автор ответа:
0
А вот тут частное решение с данными параметрами не найти.
Похожие вопросы
Предмет: Литература,
автор: Saimov
Предмет: Алгебра,
автор: serikdias67
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: RozaliMins
Предмет: Қазақ тiлi,
автор: gulsatprimbetova0