Предмет: Геометрия,
автор: Sevenskt
Один з катетів прямокутного трикутника =12см а радіус описаного навколо цього трикутника коло дорівнює 6.5 обчислити площу трикутника
Ответы
Автор ответа:
3
Дано:
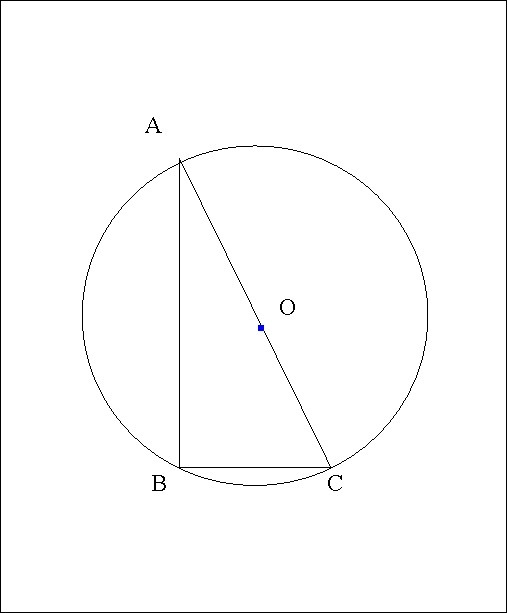
ΔАВС
∠В=90°
АВ = 12 см
R = 6,5 cм
S ΔABC
Решение
1) В прямоугольном треугольнике гипотенуза AC является диаметром D описанной окружности.
Диаметр D равен двойному радиусу 2R.
AC = D = 2R
AC = 2 · 6,5 cм = 13 см
2) По теореме Пифагора из ΔАВС найдём второй катет ВС.
ВС² = АС² - АВ²
ВС² = 13² - 12² = 169 - 144 = 25
ВС = √25 = 5
3) Площадь прямоугольного треугольника равна половине произведения катетов.
S = ab/2
S = 12·5/2=60/2=30 см²
Ответ: 30 см²
ΔАВС
∠В=90°
АВ = 12 см
R = 6,5 cм
S ΔABC
Решение
1) В прямоугольном треугольнике гипотенуза AC является диаметром D описанной окружности.
Диаметр D равен двойному радиусу 2R.
AC = D = 2R
AC = 2 · 6,5 cм = 13 см
2) По теореме Пифагора из ΔАВС найдём второй катет ВС.
ВС² = АС² - АВ²
ВС² = 13² - 12² = 169 - 144 = 25
ВС = √25 = 5
3) Площадь прямоугольного треугольника равна половине произведения катетов.
S = ab/2
S = 12·5/2=60/2=30 см²
Ответ: 30 см²
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: natalikuropat83t
Предмет: Алгебра,
автор: viktys8
Предмет: Алгебра,
автор: viktys8
Предмет: Математика,
автор: kurmaniiznurbaulet
Предмет: Музыка,
автор: goodcgool