Question

Найдите площадь фигуры, ограниченной прямыми 3x+5y=15 и x-y=-1 и осями координат

Answer 1

3x+5y=15   y=3-0,8x
x-y=-1         y=x+1
x=0
y=0
3-0,8x=x+1
1,8x=2
x=10/9
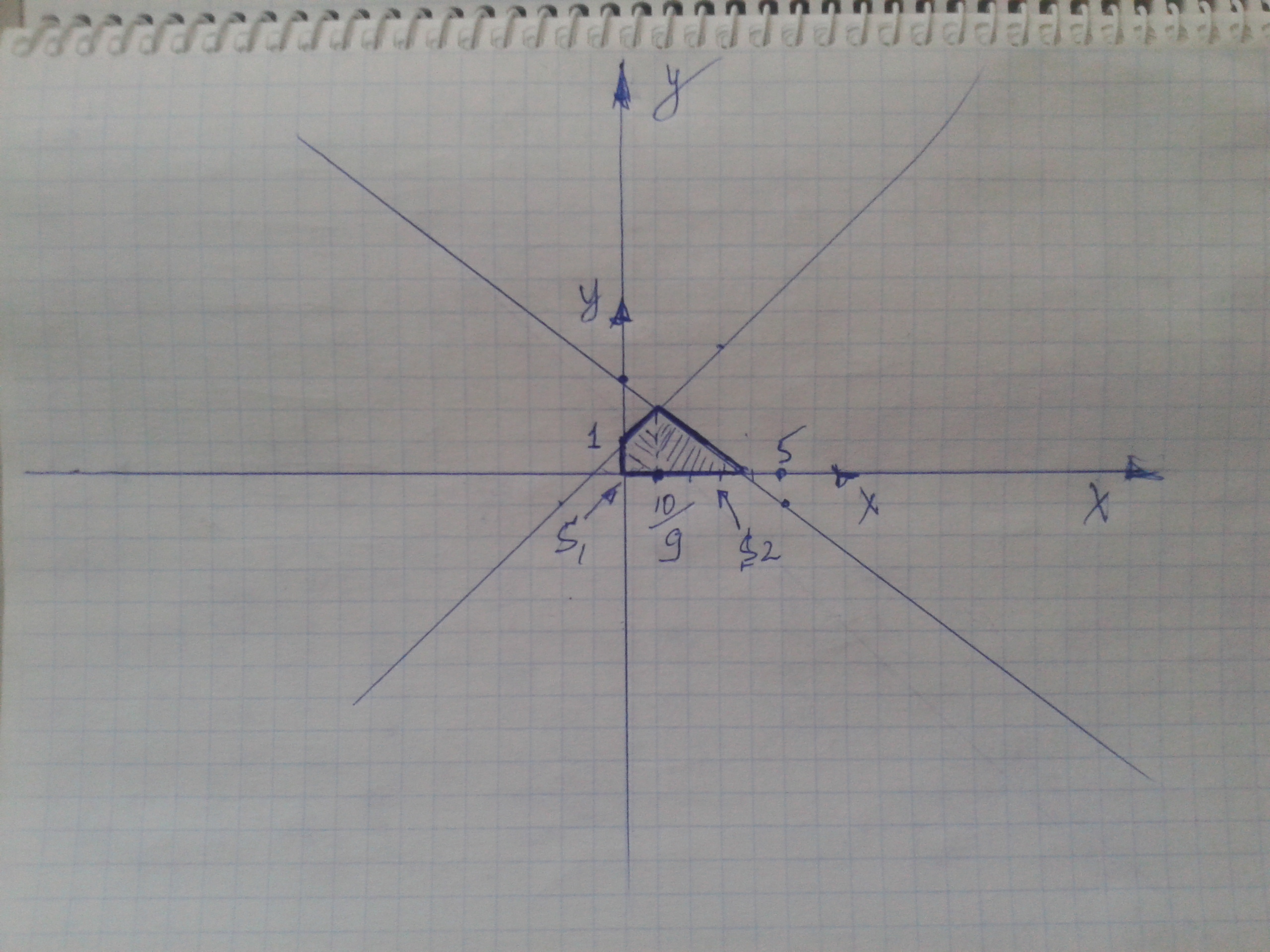
Разделим площадь на две части( см. рисунок)
S=S₁+S₂=₀∫¹⁰/⁹(x+1)dx+₁₀/₉∫³(3-0,8x)dx
S₁=(x²/2+x) |¹⁰/⁹₀=(10/9)²/2+(10/9)-01=50/81+10/9=140/81≈1,73.
S₂=3x-0,4*x² |³₁₀/₉=(3*3-0,4*3²-(3*(10/9)-0,4*(10/9)²)=
=27/5-230/81=1037/405≈2,56.   
S=S₁+S₂≈1,73+2,56≈4,29.
Ответ: S≈4,29 кв. ед.