Предмет: Математика,
автор: yugolovin
Пространство закрашено в четыре цвета. Доказать, что найдутся две точки, расстояние между которыми 1 м, закрашенные в один цвет.
Ответы
Автор ответа:
0
Допустим что две точки лежащие на расстоянии 1 м разного цвета,
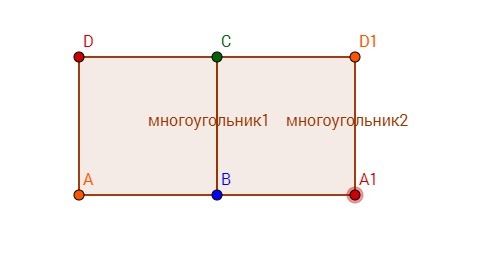
построим квадрат со стороной 1м , тогда получим что все точки принадлежашие вершинам разного цвета.
отметим точку А1 и D1 симметричную соответственно точке А и D относительно стороны ВС ,
а так как А1 находится от точек В и D1 на расстоянии 1м она не совпадает с ними по цвету , значит она совпадает по цвету с точкой А либо С , либо D
,то есть если начертить окружность с радиусом 2 ,и центром в точке А, либо окружность с радиусом √2 с центром в точке С , либо кружность с радиусом √ 5 с центром в точке D,то все точки принадлежащие этой окружности будут одного цвета , значит найдутся две точки расстояние между которыми равно 1. .Получили противоречие.
построим квадрат со стороной 1м , тогда получим что все точки принадлежашие вершинам разного цвета.
отметим точку А1 и D1 симметричную соответственно точке А и D относительно стороны ВС ,
а так как А1 находится от точек В и D1 на расстоянии 1м она не совпадает с ними по цвету , значит она совпадает по цвету с точкой А либо С , либо D
,то есть если начертить окружность с радиусом 2 ,и центром в точке А, либо окружность с радиусом √2 с центром в точке С , либо кружность с радиусом √ 5 с центром в точке D,то все точки принадлежащие этой окружности будут одного цвета , значит найдутся две точки расстояние между которыми равно 1. .Получили противоречие.
Приложения:
Автор ответа:
0
ты где этих задач накопал ))
Автор ответа:
0
Это задачи моего детства
Автор ответа:
0
А твое рассуждение я совершенно не понял
Автор ответа:
0
а ты рисуй ,читая предположим что точек одного цвета расстояние между которыми 1 м. нет тогда при построении квадрата со стороной 1 м получим вершины разных цветов , (если до ближайших по 1 перту то до противоположной приблизительно 1,4 )
Автор ответа:
0
*по 1 метру
Похожие вопросы
Предмет: Русский язык,
автор: 20fantik202009
Предмет: Английский язык,
автор: asagantay45
Предмет: Другие предметы,
автор: dashaglukhikh
Предмет: Алгебра,
автор: izmaylova1994
Предмет: Алгебра,
автор: a6880573