Предмет: Математика,
автор: андрейбутко
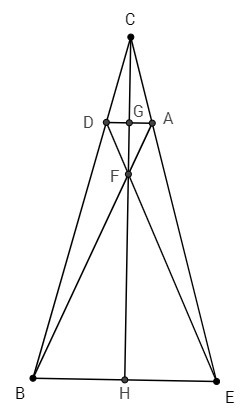
Точка А расположена на отрезке СЕ, а точка D расположена на отрезке СВ таким образом, что треугольники CАB и CDE равны, причем CD=CA=1, DВ=AЕ=3, площадь треугольника САВ равна 1. Отрезки АB и ED пересекаются в точке F. Чему равна площадь четырехугольника CAFD?
Ответы
Автор ответа:
0
CB=CE=CD+DB=4
SCAB= CA*CB*sin(BCA)/2 <=> sin(BCA)= 2*SCAB/CA*CB =0,5
∠BCE=30°
SBCE= CB*CE*sin(BCE)/2 =4
SDCA= CD*CA*sin(DCA)/2 =0,25
SBDAE= SBCE -SDCA =3,75
BE= DA*(CB/CD) = 4*DA
SBDAE= GH(BE+DA)/2 <=> GH= 2*SBDAE/(BE+DA) = 1,5/DA
FH= BE*GH/(BE+DA) =0,6/DA
SBCE= BE*CH/2 <=> CH= 2/DA
CF= CH-FH =0,8/DA
SCAFD= CF*DA*sin90°/2 =0,4
SCAB= CA*CB*sin(BCA)/2 <=> sin(BCA)= 2*SCAB/CA*CB =0,5
∠BCE=30°
SBCE= CB*CE*sin(BCE)/2 =4
SDCA= CD*CA*sin(DCA)/2 =0,25
SBDAE= SBCE -SDCA =3,75
BE= DA*(CB/CD) = 4*DA
SBDAE= GH(BE+DA)/2 <=> GH= 2*SBDAE/(BE+DA) = 1,5/DA
FH= BE*GH/(BE+DA) =0,6/DA
SBCE= BE*CH/2 <=> CH= 2/DA
CF= CH-FH =0,8/DA
SCAFD= CF*DA*sin90°/2 =0,4
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: voronenkoroma85
Предмет: Алгебра,
автор: krivykhnikita
Предмет: Информатика,
автор: MatveyMakarov
Предмет: Литература,
автор: aliskamycay1