Предмет: Геометрия,
автор: EsyaSh2130
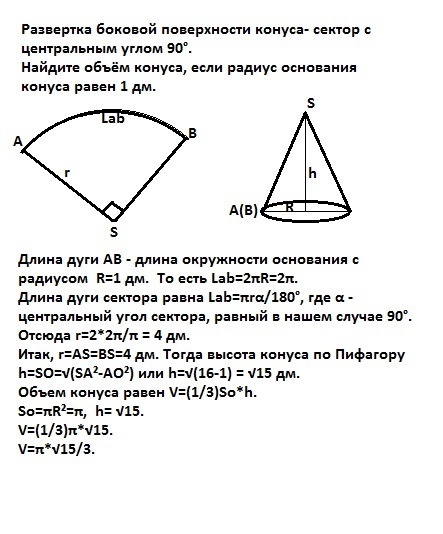
Развертка боковой поверхности конуса- сектор с центральным углом 90°.
Найдите объём конуса, если радиус основания конуса равен 1 дм.
Ответы
Автор ответа:
0
Длина дуги АВ - длина окружности основания с радиусом R=1 дм. То есть Lab=2πR=2π.Длина дуги сектора равна Lab=πrα/180°, где α - центральный угол сектора, равный в нашем случае 90°. Отсюда r=2*2π/π = 4 дм. Итак, r=AS=BS=4 дм. Тогда высота конуса по Пифагоруh=SO=√(SA²-AO²) или h=√(16-1) = √15 дм.Объем конуса равен V=(1/3)So*h.So=πR²=π дм², h= √15 дм.V=(1/3)π*√15 дм³.V=π*√15/3 дм³.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: MaksiCher2
Предмет: Геометрия,
автор: teslavitya84
Предмет: Українська мова,
автор: romansushko17
Предмет: Литература,
автор: aliskamycay1
Предмет: Музыка,
автор: Яна8811