Question

постройте график функции y=1/2(|x/1,5-1,5/x|+x/1,5+1,5/x) и определите при каких значениях m прямая y=m имеет с графиком ровно одну общую точку
срочно помогите!

Answer 1

Сначала приведем функцию в более простую форму.
y = 1/2*(|x/(3/2) - (3/2)/x| + x/(3/2) + (3/2)/x) = 1/2*(|2x/3 - 3/(2x)| + 2x/3 + 3/(2x))
y = |x/3 - 3/(4x)| + x/3 + 3/(4x)

1) Пусть x/3 - 3/(4x) < 0, то есть
(4x^2 - 9)/(12x) < 0
(2x + 3)(2x - 3)/(12x) < 0
x ∈ (-oo; -3/2) U (0; 3/2)

Тогда |x/3 - 3/(4x)| = 3/(4x) - x/3
y = 3/(4x) - x/3 + x/3 + 3/(4x) = 3/(4x) + 3/(4x) = 3/(2x)
y(-3/2) = 3/2 : (-3/2) = -1 - это точка минимума

2) Пусть x/3 - 3/(4x) >= 0, то есть
Точно также получаем
x ∈ [-3/2; 0) U [3/2; +oo)

Тогда |x/3 - 3/(4x)| = x/3 - 3/(4x)
y = x/3 - 3/(4x) + x/3 + 3/(4x) = 2x/3
y(3/2) = 2/3*3/2 = 1 - это тоже точка минимума.
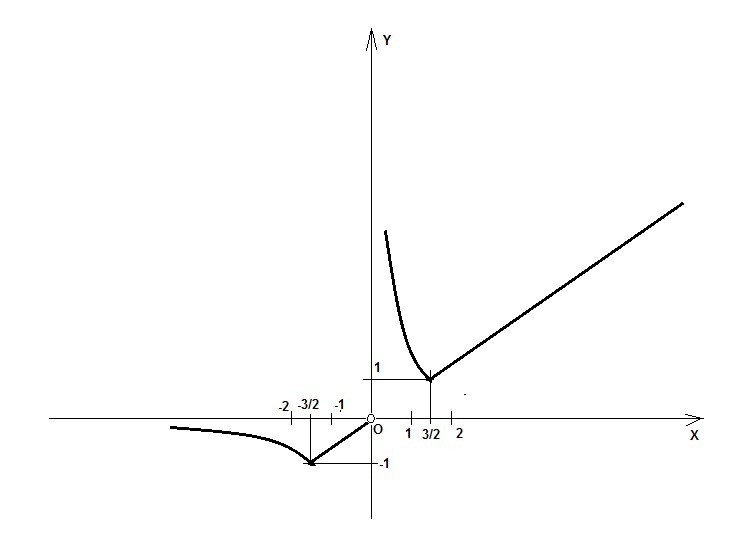
В этих двух точках и будет одно пересечение с прямой y = m
Вот на рисунке примерный график этой функции.