Question

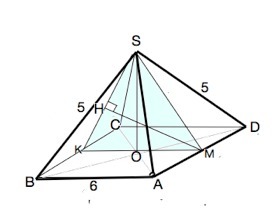
В правильной четырёхугольной пирамиде SABCD (с вершиной S) сторона основания равна 6, а боковое ребро равно 5. Найдите расстояние от точки A до плоскости BCS

Answer 1

Диагональ AC=BD = 6√2
Половина диагонали OC=OD=OA=OB=3√2
Из треугольника SOA высота SO=√(5^2-(3√2)^2)=√7
Поместим центр координат в точку B ось X - BA  ось Y - BC  ось Z - вверх от B параллельно OS
Тогда координаты интересующих нас точек будут B(0;0;0) C(0;6;0) S(3;3;√7) A(6;0;0)
Плоскость BCS проходит через 0 - посему ее уравнение ax+by+cz=0 подставим координаты точек в уравнение
b=0
3a+3b+√7c=0
положим a=1 тогда с=-3/√7

x-3/√7z=0
Нормализованное уравнение плоскости k=√(1+9/7)=4/√7
√7/4*x-3/4*z=0
подставим координаты точки A(6;0;0) в нормализованное уравнение
l = 6√7/4=3√7/2  - это искомое расстояние до плоскости.

Answer 2

Вариант решения. 

Точка А принадлежит прямой AD. Прямая AD параллельна ВС, следовательно, параллельна плоскости BSC, поэтому все её точки  находятся на одинаковом расстоянии от этой плоскости.  

Проведем в противоположных  гранях пирамиды сечение  через апофемы   SK и SM.

М - основание апофеы на AD, AM=DM=3.

SM=SK=4 ( ∆ ASM - египетский.

В ∆ SOK  по т.Пифагора SO=√(SK²-OK²)=√(16-9)=√7

sin∠SKO=SO:SK=√7/4

Искомое расстояние от точки М до плоскости - длина отрезка МН, проведенного к ней  перпендикулярно, оно равно расстоянию от А до той же плоскости (см. выше). 

МН=КМ•sin∠SKO=6•√7/4=3√7/2