Question

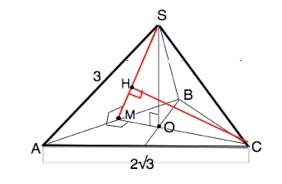
В правильной треугольной пирамиде SABC (с вершиной S) сторона основания равна 2√3, а боковое ребро равно 3. Найдите расстояние от точки C до плоскости ABS.
Ответ должен получится√(15/2)

Answer 1

Расстояние от точки до плоскости равно длине отрезка, проведенного перпендикулярно к этой плоскости. 

Проведем через ребро SC и высоту пирамиды плоскость перпендикулярно плоскости ASB.

SM⊥АВ и СМ⊥АВ. Отрезок СН лежит в плоскости MSC, он перпендикулярен линии пересечения плоскостей SM  ⇒

 CH перпендикулярен плоскости ASB 

Искомое расстояние равно длине СН. 

Основание правильной треугольной пирамиды - правильный треугольник. Все его стороны равны, все углы равны 60°⇒

1)  СМ=АС•sin60°=2√3•√3:2=3

2) SM=√(SA²-AM²) 

AM=AB:2=√3

SM=√(9-3) =√6

3) SO=√(SM²-OM²)

OM=CM:3 =1( медианы точкой пересечения делятся в отношении 2:1) 

SO=√(6-1)=√5

4) sin ∠SMC=SO:SM=√5:√6

5) CH=CM•sin SMC=3•√5:√6=(√5•√2•√3):2=√15:√2 или √(15/2)