Предмет: Математика,
автор: AdeleKot
В трапеции ABCD известно,что AD=4,BC=2,а ее площадь равна 60.Найдите площадь трапеции BCNM,где MN-средняя линия трапеции ABCD.
Ответы
Автор ответа:
0
Ответ:
25 см²
Пошаговое объяснение:
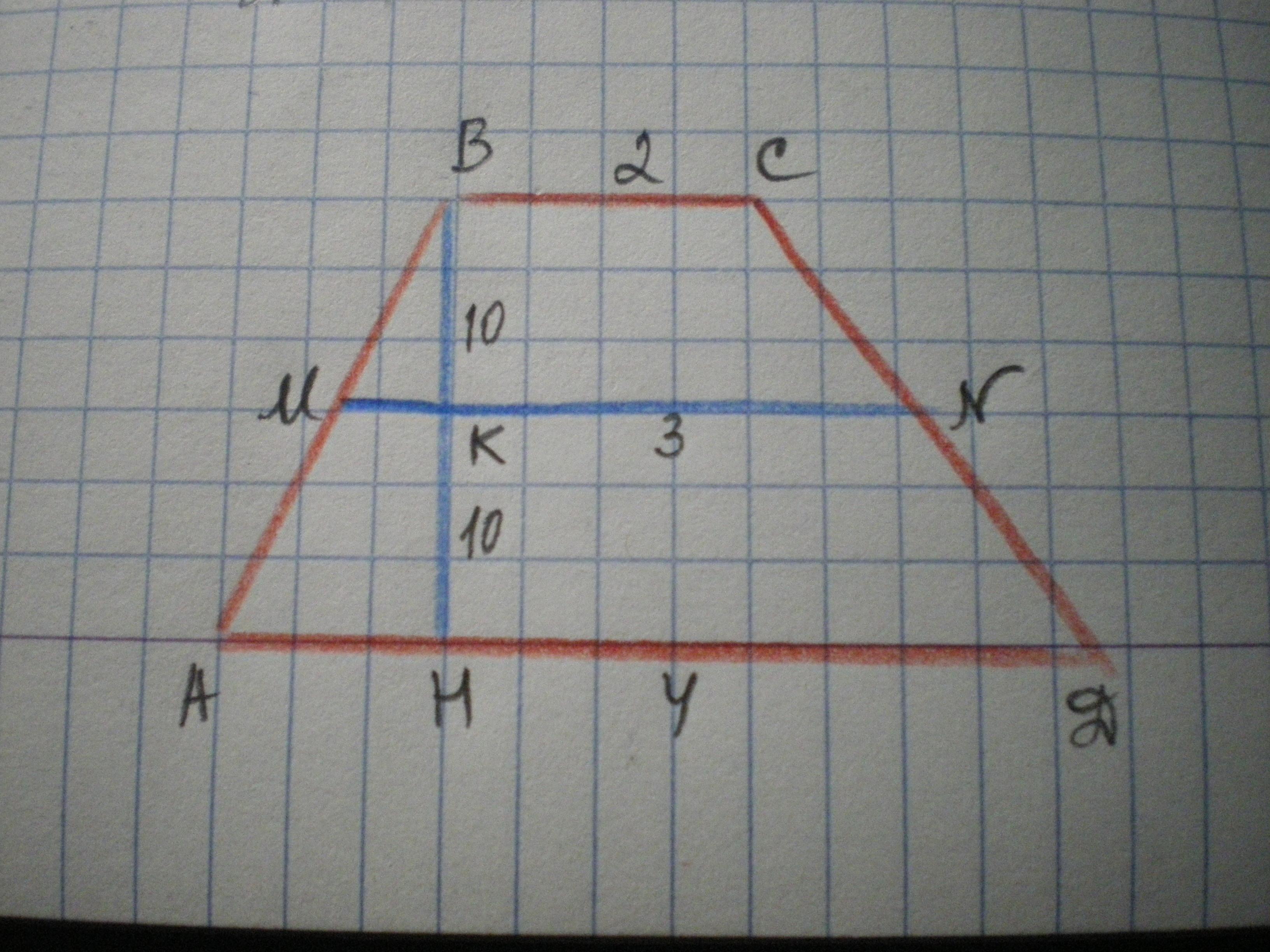
Дано: ABCD - трапеция, AD=4 см, BC=2 см, S=60 см², МN - средняя линия. Найти S(BCNM).
Решение: МN=(АD+ВС)/2=(2+4)/2=3 см.
Проведем высоту ВН. Найдем ВН из формулы S=MN*BH
60=3ВH; BH=20 cм.
Найдем S(BCNM)=(ВС+MN)/2 * ВК.
ВК=1/2 ВН, т.к. MN - средняя линия и делит ВН пополам.
ВК=20:2=10 см.
S(BCNM)=(2+3)/2 * 10 = 25 см²
Приложения:
Похожие вопросы
Предмет: История,
автор: sesjsja
Предмет: Математика,
автор: kapralovaulana42
Предмет: Литература,
автор: kotK10
Предмет: Математика,
автор: solmasusupova
Предмет: Литература,
автор: tanyatanyaaya