Предмет: Математика,
автор: тралиса155
Исследуйте функцию с помощью производной на монотонность и экстремумы
Y=4x^3-12x+5
Ответы
Автор ответа:
0
Исследование:
1) Область определения и область значения функции

Область определения (-оо;+оо)
Область значения (-oo;+oo)
2) Исследуем общие свойства функции: чётность; нечётность

Значит функция не является ни четной ни нечетной
3) Находим точки пересечения графика функции с осями координат.

точка пересечения с осью Оу (0;5)

Уравнение в целых числах не решается:
х₁≈-1,9; х₂≈0,44; х₃≈1,46
Точки пересечения с осью Ох (-1,9;0) (0,44;0) (1,46;0)
4) Находим критические точки и интервалы монотонности.
для этого найдем производную

найдем критические точки

определим знаки производной
+ - +
-------- -1 ------------ 1 --------------
на интервале (-оо; -1 ) (1;+оо) возрастает
на интервале (-1;1) убывает
точка х= -1 - точка максимума
 максимум функции
максимум функции
точка х=1 - точка минимума
 минимум функии
минимум функии
5) Найдем точки перегиба и интервалы выпуклости.
Для этого найдем вторую производную

найдем критические точки

определим знаки второй производной на интервалах
- +
------------ 0 --------------
На интервале (-оо;0) график Выпуклый вверх
на интервале (0;+оо) график выпуклый вниз-вогнутый
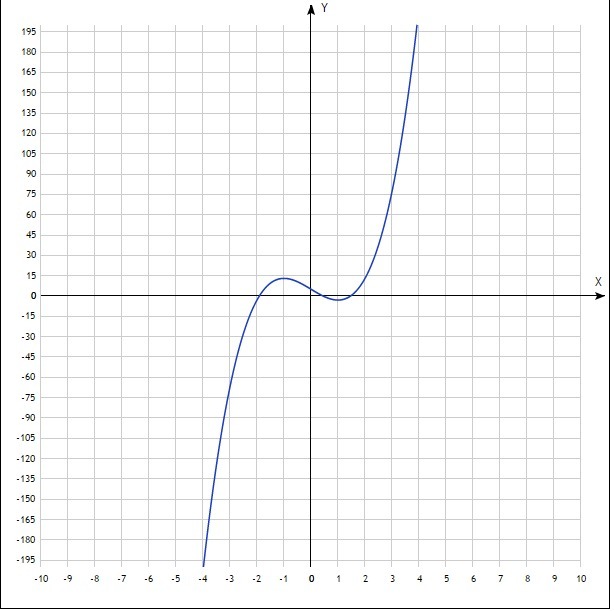
и график в приложении
1) Область определения и область значения функции
Область определения (-оо;+оо)
Область значения (-oo;+oo)
2) Исследуем общие свойства функции: чётность; нечётность
Значит функция не является ни четной ни нечетной
3) Находим точки пересечения графика функции с осями координат.
точка пересечения с осью Оу (0;5)
Уравнение в целых числах не решается:
х₁≈-1,9; х₂≈0,44; х₃≈1,46
Точки пересечения с осью Ох (-1,9;0) (0,44;0) (1,46;0)
4) Находим критические точки и интервалы монотонности.
для этого найдем производную
найдем критические точки
определим знаки производной
+ - +
-------- -1 ------------ 1 --------------
на интервале (-оо; -1 ) (1;+оо) возрастает
на интервале (-1;1) убывает
точка х= -1 - точка максимума
точка х=1 - точка минимума
5) Найдем точки перегиба и интервалы выпуклости.
Для этого найдем вторую производную
найдем критические точки
определим знаки второй производной на интервалах
- +
------------ 0 --------------
На интервале (-оо;0) график Выпуклый вверх
на интервале (0;+оо) график выпуклый вниз-вогнутый
и график в приложении
Приложения:
Автор ответа:
0
Спасибо большое
Похожие вопросы
Предмет: Английский язык,
автор: Math3227
Предмет: Физика,
автор: supermedic007
Предмет: Русский язык,
автор: utelbaeva0110
Предмет: Математика,
автор: зак6
Предмет: Биология,
автор: Аноним