Предмет: Математика,
автор: vldislavgit
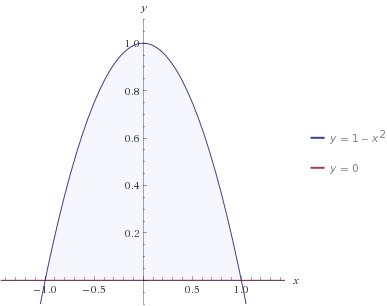
Найдите площадь фигуры ограниченной графиками функций y=1-x^2 и осью абсцисс.
Ответы
Автор ответа:
0
ищем пределы интегрирования:

И находим площадь с помощью определенного интеграла:

Ответ: ед²
ед²
И находим площадь с помощью определенного интеграла:
Ответ:
Приложения:
Автор ответа:
0
Что еще за tex?
Автор ответа:
0
обновите страницу
Автор ответа:
0
Спасибо)
Похожие вопросы
Предмет: Математика,
автор: canya69
Предмет: Математика,
автор: he040784liv
Предмет: Информатика,
автор: Аноним
Предмет: Химия,
автор: akbotaumirhanova