Предмет: Геометрия,
автор: Victorienel6151
Радиус вписанной в ромб окружности равен 5,а один из углов ромба равен 60 градусов.Найти длину большей диагонали ромба.
Пожалуйста ,можно с пояснениями
Ответы
Автор ответа:
0
])))))))))))))))))))))))))
Приложения:
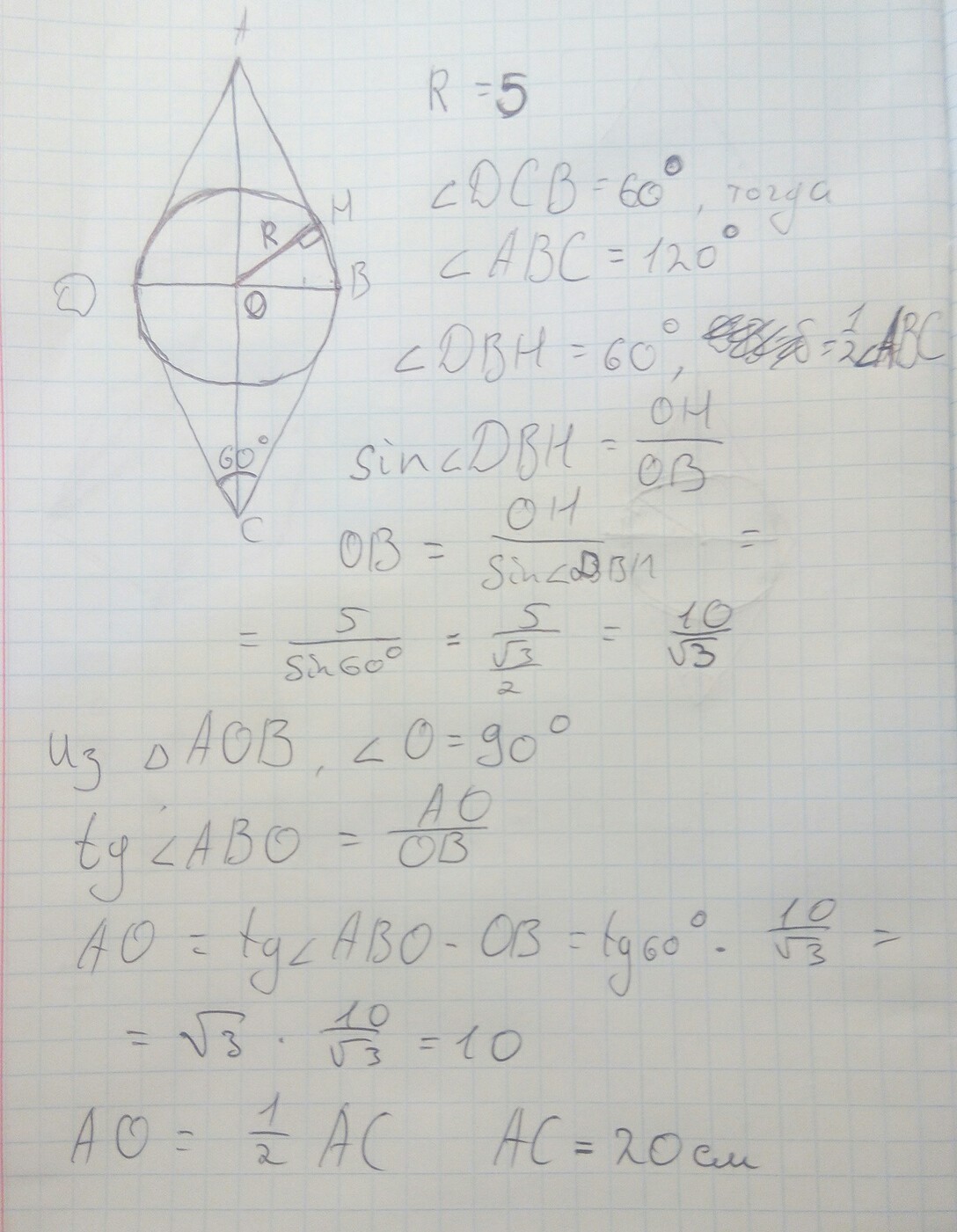
Автор ответа:
0
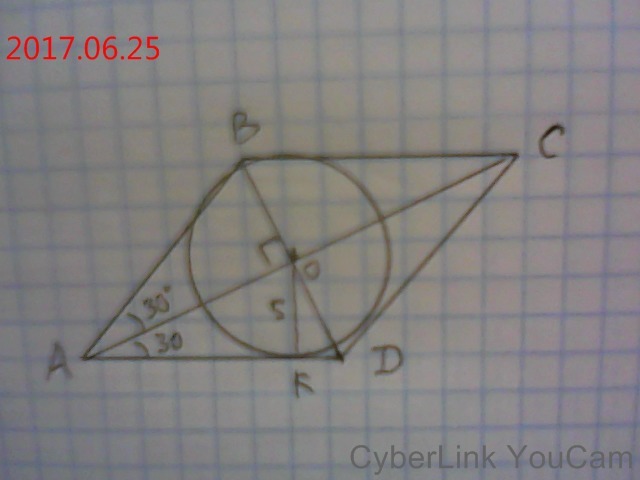
АВСD - ромб: АВ=ВС=СD=АD.
точка О - центр вписанной окружности; ОК - радиус этой окружности. ОК=5
По условию ∠ВАС=60·. Диагонали ромба являются биссектрисами его углов; значит ∠САD=30°.
ΔАОК; АК⊥АD, ОК=5 см. ОК лежит против угла 30°, значит гипотенуза АО в два раза больше этого катета АО=2·5=10 см.
Диагонали ромба пересекабтся и тоской пересечения делятся пополам.Значит АО=ОС= 10 см, АС=10+10=20 см.
Диагональ ВD <АС так как АО<ОD.
Ответ: 20 см.
точка О - центр вписанной окружности; ОК - радиус этой окружности. ОК=5
По условию ∠ВАС=60·. Диагонали ромба являются биссектрисами его углов; значит ∠САD=30°.
ΔАОК; АК⊥АD, ОК=5 см. ОК лежит против угла 30°, значит гипотенуза АО в два раза больше этого катета АО=2·5=10 см.
Диагонали ромба пересекабтся и тоской пересечения делятся пополам.Значит АО=ОС= 10 см, АС=10+10=20 см.
Диагональ ВD <АС так как АО<ОD.
Ответ: 20 см.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: mezenbekovau
Предмет: Алгебра,
автор: kolppan
Предмет: Математика,
автор: kamronmamatov550
Предмет: Обществознание,
автор: 197319621993
Предмет: История,
автор: yyyyps