Предмет: Математика,
автор: surfs1
Решить неопределенный интеграл, заранее большое спасибо
Приложения:
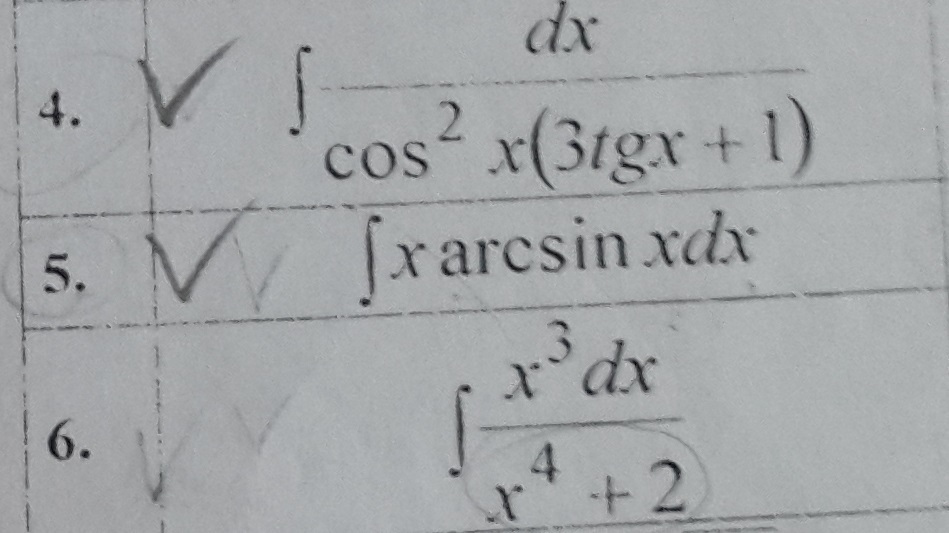
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: mirakurmambayeva
Предмет: Математика,
автор: damirsabanaev1
Предмет: Математика,
автор: derevyanko0059
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: эмилия20