Предмет: Алгебра,
автор: muhamadx
РЕШИТЕ ПОЖАЛУЙСТА ИРРАЦИОНАЛЬНОЕ УРАВНЕНИЕ!!!
Приложения:

Ответы
Автор ответа:
0
Проверим ОДЗ. x^2+24>=0 xЄ(-бесконеч.; +бесконеч.)
6-x^2>=0 x^2=<6 xЄ[-√6; √6].
Общее ОДЗ xЄ[-√6; √6]
Возведём во вторую степень обе части равенства.
x^2+24=(6-x^2)^2
x^2+24=6^2-2*6*x^2+(x^2)^2
x^2+24=36-12*x^2+x^4
x^4-12*x^2-x^2+36-24=0
x^4-13*x^2+12=0
Пусть x^2=t
t^2-13*t+12=0 t1,2=(13±√(13^2-4*12))/2=(13±11)/2
t1=(13-11)/2=1 x^2=1 x=±1
t2=(13+11)/2=12 x^2=12 x=±√12 не отвечает ОДЗ
Ответ х=±1
6-x^2>=0 x^2=<6 xЄ[-√6; √6].
Общее ОДЗ xЄ[-√6; √6]
Возведём во вторую степень обе части равенства.
x^2+24=(6-x^2)^2
x^2+24=6^2-2*6*x^2+(x^2)^2
x^2+24=36-12*x^2+x^4
x^4-12*x^2-x^2+36-24=0
x^4-13*x^2+12=0
Пусть x^2=t
t^2-13*t+12=0 t1,2=(13±√(13^2-4*12))/2=(13±11)/2
t1=(13-11)/2=1 x^2=1 x=±1
t2=(13+11)/2=12 x^2=12 x=±√12 не отвечает ОДЗ
Ответ х=±1
Автор ответа:
0
Решение данного задания
Приложения:
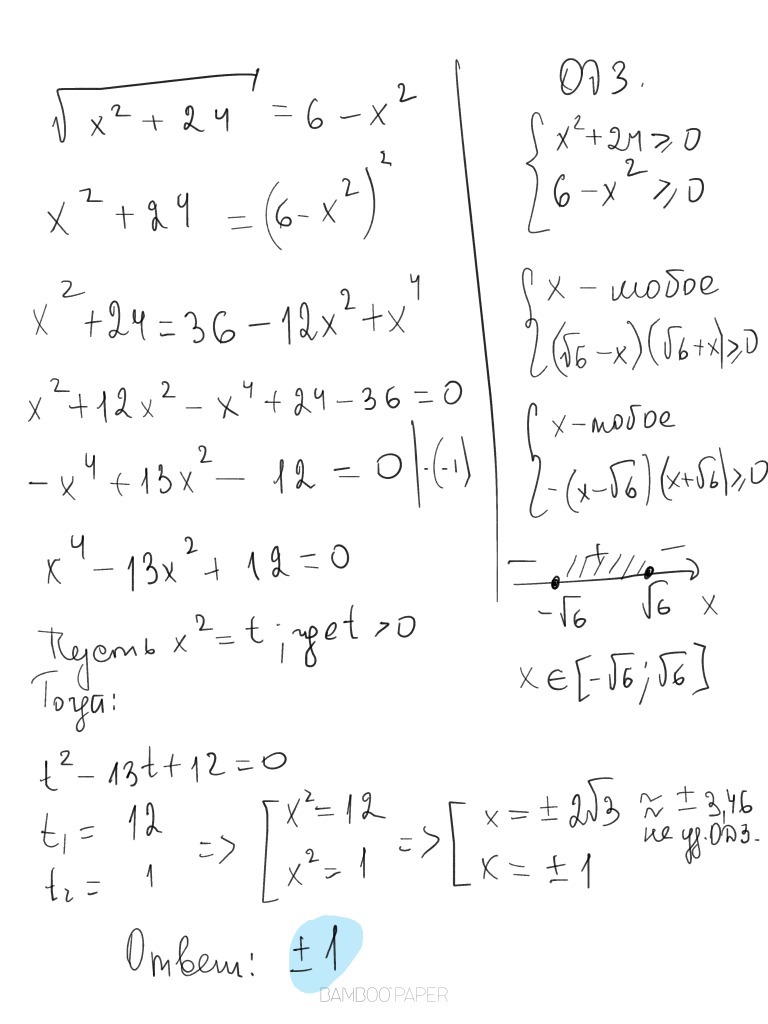
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: naduaksv
Предмет: Английский язык,
автор: kuvantaevabekzada
Предмет: Информатика,
автор: эльза54
Предмет: Математика,
автор: NikNikitaI