Question

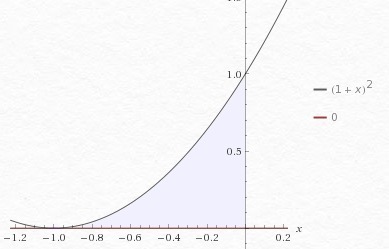
Вычислите площадь фигуры, ограниченной графиками функций:
у=(х+1)^2, у=0, х=0

Answer 1

у=(х+1)^2, у=0 (ось оX)
, х=0
S=$intlimits^a_b {x} , dx$
найдем 2-й предел
(x+1)^2=0
x=-1
S=∫0,-1(x+1)^2dx=|0,-1((x+1)^3)/3=1/3-0=1/3

Answer 2

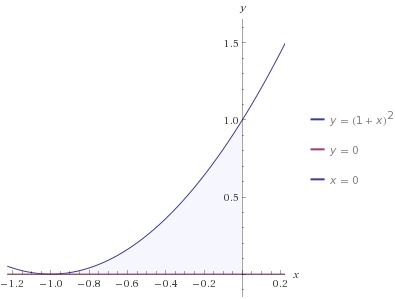
первый предел есть: x=0
ищем 2 предел:
(x+1)^2=0
x+1=0
x=-1
(x+1)^2=x^2+2x+1
находим площадь с помощью определенного интеграла:
$intlimits^0_{-1} {(x^2+2x+1)} , dx= (frac{x^3}{3}+x^2+x )intlimits^0_{-1}=0-( -frac{1}{3}+1-1)= frac{1}{3}$
Ответ: $S(G)= frac{1}{3}$