Предмет: Математика,
автор: quasar4
Вычислить задания номер 1 и 2 дам 20 баллов
Приложения:
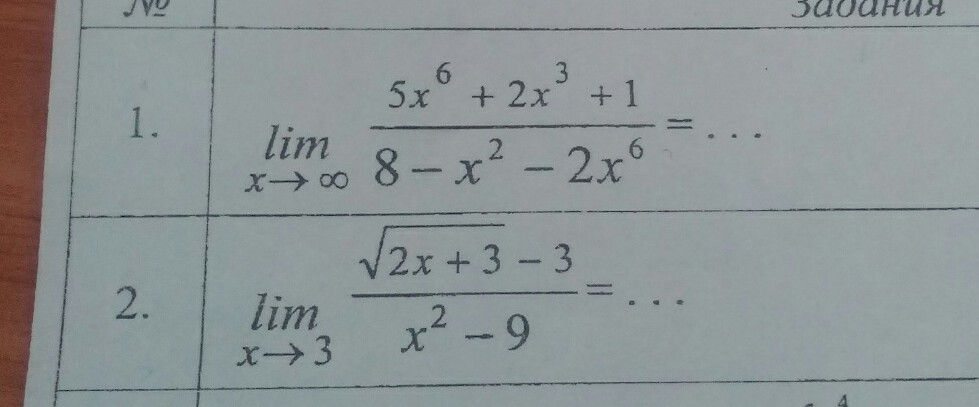
Ответы
Автор ответа:
0
1) имеем неопределенность oo/oo.
поделим числитель и знаменатель на :
:

2)имеем неопределенность 0/0.
умножаем данную дробь на сопряженное выражение, в данном случае на ( ):
):

поделим числитель и знаменатель на
2)имеем неопределенность 0/0.
умножаем данную дробь на сопряженное выражение, в данном случае на (
Похожие вопросы
Предмет: Другие предметы,
автор: fedorovich05
Предмет: Биология,
автор: Nizam15
Предмет: Алгебра,
автор: berlogamedvedya
Предмет: Литература,
автор: lannifam2015