Предмет: Математика,
автор: Vikysik3211
Помогите пожалуесто решить мне показательные уравнения
Приложения:
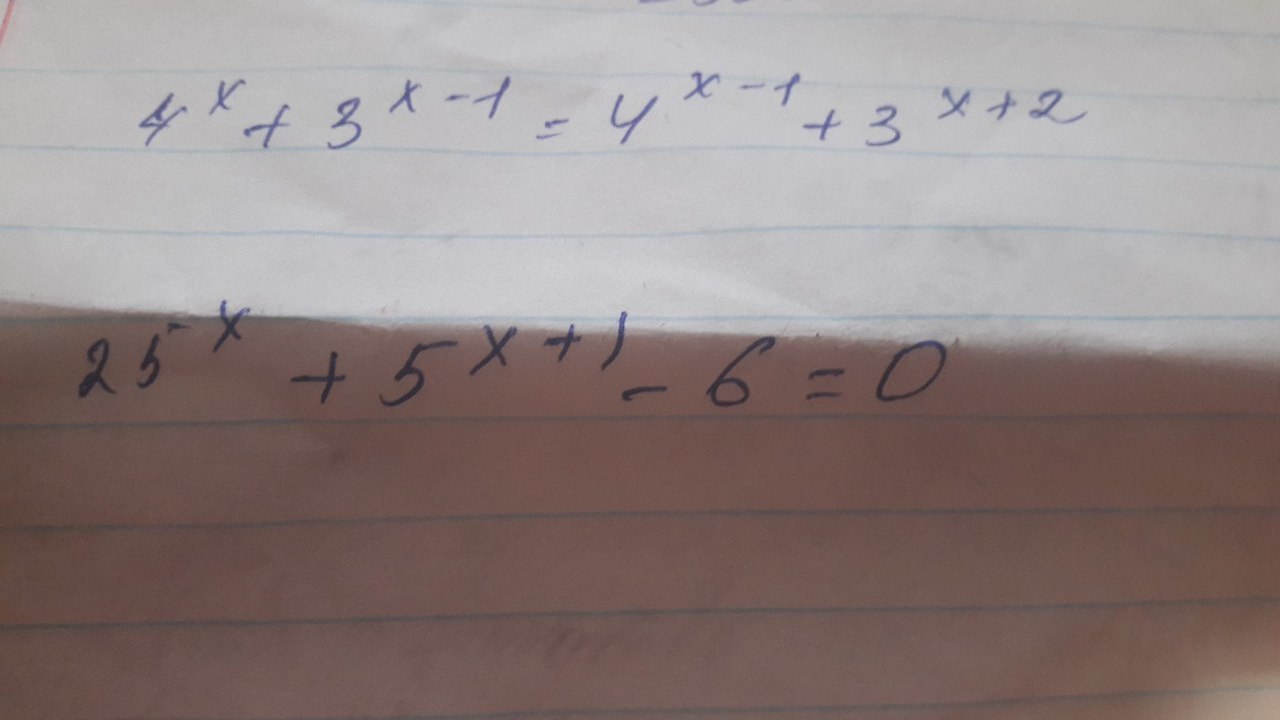
Ответы
Автор ответа:
0
1) 4ˣ - 4ˣ⁻¹ = 3ˣ⁺² - 3ˣ⁻¹
4ˣ⁻¹(4 - 1) = 3ˣ⁻¹(3³ -1)
4ˣ⁻¹ *3 = 3ˣ⁻¹ * 26 | : (3ˣ⁻¹ * 3)
(4/3)ˣ⁻¹ = 26/3
2) Учтём, что 25 = 5² и 5ˣ⁺¹ = 5ˣ *5¹
Введём новую переменную: 5ˣ = t
t² +5t -6 = 0
По т. Виета корни - 6 и 1
а)5ˣ = -6 б) 5ˣ = 1
∅ х = 0
4ˣ⁻¹(4 - 1) = 3ˣ⁻¹(3³ -1)
4ˣ⁻¹ *3 = 3ˣ⁻¹ * 26 | : (3ˣ⁻¹ * 3)
(4/3)ˣ⁻¹ = 26/3
2) Учтём, что 25 = 5² и 5ˣ⁺¹ = 5ˣ *5¹
Введём новую переменную: 5ˣ = t
t² +5t -6 = 0
По т. Виета корни - 6 и 1
а)5ˣ = -6 б) 5ˣ = 1
∅ х = 0
Автор ответа:
0
в 1-м примере не дорешал, что-то с условием не так...
Автор ответа:
0
вот и я думаю, ошибка там в условии
Автор ответа:
0
1. 4^x+3^(x-1)=4^(x-1)+3^(x+2)
4^x-4^(x-1)=3^(x+2)-3^(x-1)
4^x-4^x/4=9*3^x-3^x/3
4^x*(1-1/4)=3^x*(9-1/3)
4^x*(3/4)=3^x*(26/3)
(4^x)/(3^x)=(26/3)/(3/4) так как степени в дроби одинаковы, то
(4/3)^x=(26*4)/(3*3)
(4/3)^x=104/9
x=loq4/3(104/9)
2. 25^x+5^(x+1)-6=0
5^2*x+5*5^x-6=0
Пусть 5^x=y
y^2+5*y-6=0
y1,2=(-5±√(5^2+4*6))/2=(-5±7)/2
y1=(-5-7)/2=-6 не подходит так как 5^x>0
y2=(-5+7)/2=1 5^x=1 5^x=5^0 x=0
4^x-4^(x-1)=3^(x+2)-3^(x-1)
4^x-4^x/4=9*3^x-3^x/3
4^x*(1-1/4)=3^x*(9-1/3)
4^x*(3/4)=3^x*(26/3)
(4^x)/(3^x)=(26/3)/(3/4) так как степени в дроби одинаковы, то
(4/3)^x=(26*4)/(3*3)
(4/3)^x=104/9
x=loq4/3(104/9)
2. 25^x+5^(x+1)-6=0
5^2*x+5*5^x-6=0
Пусть 5^x=y
y^2+5*y-6=0
y1,2=(-5±√(5^2+4*6))/2=(-5±7)/2
y1=(-5-7)/2=-6 не подходит так как 5^x>0
y2=(-5+7)/2=1 5^x=1 5^x=5^0 x=0
Автор ответа:
0
Вспомни основную формулу: a^x=b x=loqa(b)
Автор ответа:
0
у меня вопрос не к Вашему решению, а к условию) Как у Вас получился логарифм, я понимаю, у свех решающих так получилось. Просто логически какой должна быть степень, чтоб из 4/3 получить 104/9
Автор ответа:
0
на калькуляторе 3,35022
Автор ответа:
0
У тебя есть инженерный калькулятор с функцией логарифм? Вот он так посчитал.
Автор ответа:
0
не додумалась! в экселе посчитала) спасибо
Похожие вопросы
Предмет: Информатика,
автор: sofiavanukova9
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: Hrumi
Предмет: Математика,
автор: BriarBeaty