Предмет: Алгебра,
автор: vikulyazorina
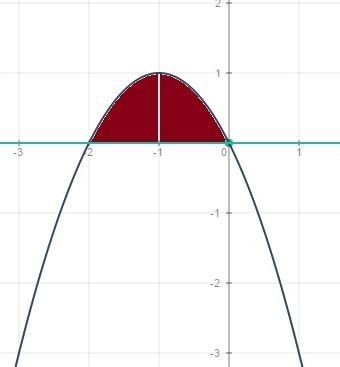
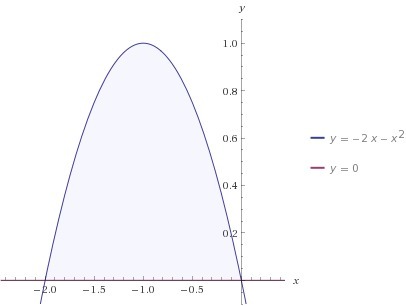
Найдите площадь фигуры ограниченной линиями y = - 2x - x², y = 0.
Ответы
Автор ответа:
0
s=F(0)-F(-2) F=∫(-2x-x²)=-x²-x³/3 F(0)=0 F(-2)=-4+8/3
s=0+4-8/3=12/3-8/3=4/3
s=0+4-8/3=12/3-8/3=4/3
Приложения:
Автор ответа:
0
Спасибо вам огромное:)
Автор ответа:
0
ищем точки пересечения:

0 и (-2) - пределы интегрирования.

Ответ: ед²
ед²
0 и (-2) - пределы интегрирования.
Ответ:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: diasnurgeldy7
Предмет: География,
автор: nd6675524
Предмет: Музыка,
автор: 15r15rh
Предмет: Математика,
автор: врмва