Предмет: Математика,
автор: 266315
Часть С
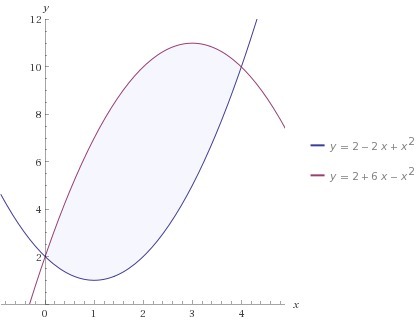
Найдите площадь плоской фигуры, ограниченой линиями y=x^2-2x+2 и y=2 +6x-x^2
Приложения:

Ответы
Автор ответа:
0
для начала ищем точки пересечения данных графиков:

x=0 и x=4 - пределы интегрирования:

Ответ:
x=0 и x=4 - пределы интегрирования:
Ответ:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: nametovadiana
Предмет: Английский язык,
автор: gabbasovadilnaz4
Предмет: Математика,
автор: 0000777827m
Предмет: Физика,
автор: lizikzueva
Предмет: Алгебра,
автор: AnnaPlotnikova2001