Предмет: Геометрия,
автор: NeverLove
Найдите площадь треугольника, образованного прямой 3х+8у-24=0 и координатными осями.
Ответы
Автор ответа:
0
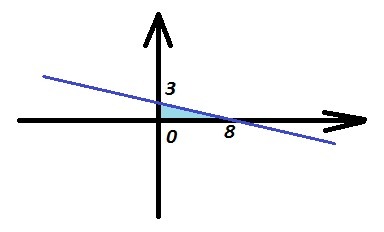
Получившийся треугольник будет прямоугольным, так как координатные оси перпендикулярны. Площадь прямоугольного треугольника равна половине произведения его катетов. Кроме того, катеты лежат на координатных осях, и один из концов каждого катета имеет координаты (0; 0).
Найдем точки пересечения прямой с осями координат.
Если х=0, то:

- точка пересечения (0; 3)
Если у=0, то:

- точка пересечения (8; 0)
Тогда длина одного катета равна 3, другого - равна 8.

Ответ: 12
Найдем точки пересечения прямой с осями координат.
Если х=0, то:
- точка пересечения (0; 3)
Если у=0, то:
- точка пересечения (8; 0)
Тогда длина одного катета равна 3, другого - равна 8.
Ответ: 12
Приложения:
Автор ответа:
0
Спасибо большое
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Окружающий мир,
автор: iyarovoy702
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: Dimassis
Предмет: Химия,
автор: аня608