Предмет: Математика,
автор: lestertrap2014
Помогите решить! (Интегралы)
Приложения:
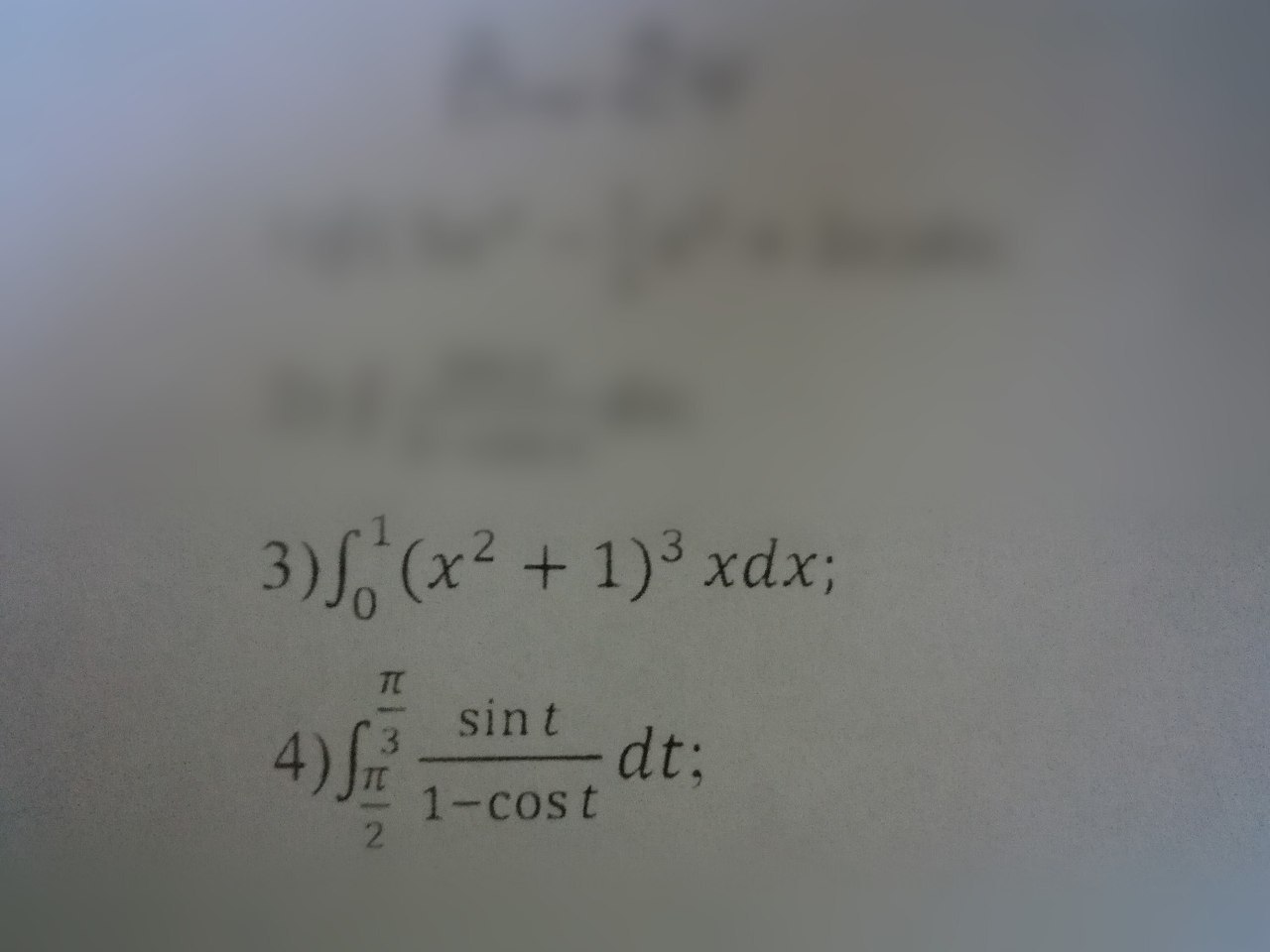
Ответы
Автор ответа:
0
integral x є [0;1] (x^2+1)^3 xdx =
1/2*integral x є [0;1] (x^2+1)^3 d(x^2) =
1/2*integral x є [0;1] (x^2+1)^3 d(x^2+1) =
x^2+1 = t; x=0 => t=1
x^2+1 = t; x=1 => t=2
1/2*integral t є [1;2] t^3 dt =
1/2*1/4 * t^4 {t є [1;2] = 1/8 * (2^4-1^4)=15/8
integral t є [pi/2;pi/3] sin(t)/(1-cos(t)) dt =
- integral t є [pi/2;pi/3] d(cos(t))/(1-cos(t)) =
integral t є [pi/2;pi/3] d(1-cos(t))/(1-cos(t)) =
1-cos(t) = x; t=pi/2 => x=1
1-cos(t) = x; t=pi/3 => x=1/2
integral x є [1;1/2] dx/x =
ln(|x|) {x є [1;1/2] =
ln(1/2) -ln(1)=
-ln2-0=
-ln(2)
1/2*integral x є [0;1] (x^2+1)^3 d(x^2) =
1/2*integral x є [0;1] (x^2+1)^3 d(x^2+1) =
x^2+1 = t; x=0 => t=1
x^2+1 = t; x=1 => t=2
1/2*integral t є [1;2] t^3 dt =
1/2*1/4 * t^4 {t є [1;2] = 1/8 * (2^4-1^4)=15/8
integral t є [pi/2;pi/3] sin(t)/(1-cos(t)) dt =
- integral t є [pi/2;pi/3] d(cos(t))/(1-cos(t)) =
integral t є [pi/2;pi/3] d(1-cos(t))/(1-cos(t)) =
1-cos(t) = x; t=pi/2 => x=1
1-cos(t) = x; t=pi/3 => x=1/2
integral x є [1;1/2] dx/x =
ln(|x|) {x є [1;1/2] =
ln(1/2) -ln(1)=
-ln2-0=
-ln(2)
Похожие вопросы