Question

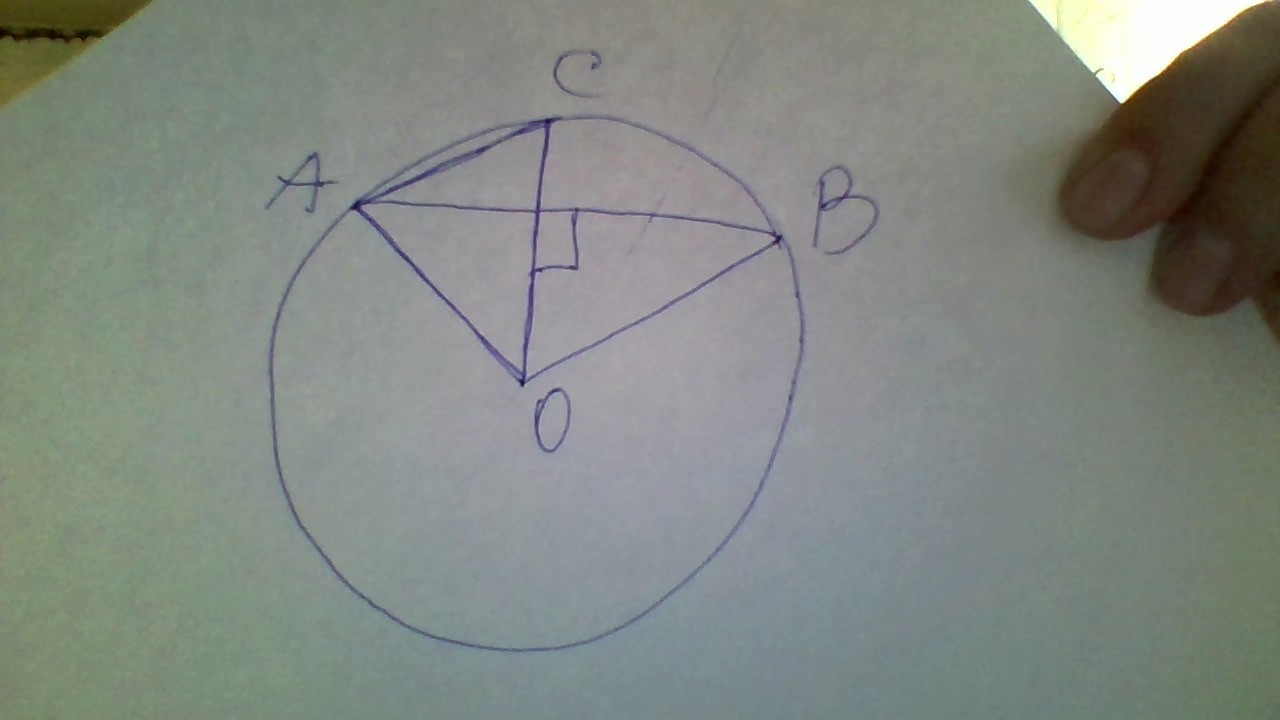
Найти углы треугольника АОС , если ОС перпендик. АВ, ОА=АВ

Answer 1

AO=BO - как радиусы одной окружности.
По условию АО=АВ, а значит АО=АВ=ВО, то есть▲АОВ - равносторонний.
<АВО=<АОВ=<ВАО=60°
Высота, проведённая из любой вершины равностороннего треугольника является медианой и биссектрисой. 
ОС∟АВ →<АОС=<СОВ=60/2=30°
▲АСО  АО=СО как радиусы одной окружности. 
▲АСО - равносторонний. <АСО=<САО
<АСО+<САО+<АОС=180°
<АСО=<САО=(180-30)/2=75°

Answer 2

Треугольник ОАВ - равносторонний, значит угол АОВ = 60, значит угол О в треугольнике АОС = 30(т.к. ОС - и высота, и медиана, и биссектриса угла О).
Если центральный угол равен 60, то вписанный угол равен 30, а вписанный с противоположной стороны = 180-30 = 150, значит угол С в треугольнике АОС = 75
Тогда угол А в треугольнике АОС = 180-(30+75) = 75
Ответ: 75; 30, 75

Answer 3

Спасибо большое