Предмет: Математика,
автор: Unknownintellegence
Вычислите определенный интеграл
Приложения:
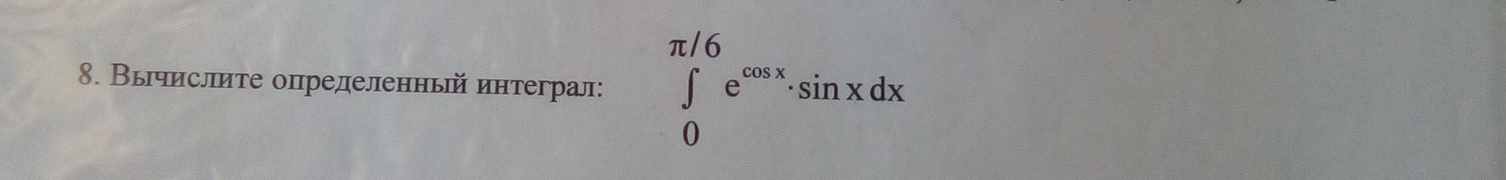
Ответы
Автор ответа:
0
Делаем замену: u=cos(x), тогда du= -sin(x) dx.
Исходный интеграл примет простой вид:
Интеграл((-e^u) du) = -e^u
Возвращаемся от u к x: Интеграл = -e^cos(x)
Подставляем пределы интегрирования:
-e^cos(pi/6)+e^cos(0) = -e^(Корень(3)/2) + e
Исходный интеграл примет простой вид:
Интеграл((-e^u) du) = -e^u
Возвращаемся от u к x: Интеграл = -e^cos(x)
Подставляем пределы интегрирования:
-e^cos(pi/6)+e^cos(0) = -e^(Корень(3)/2) + e
Автор ответа:
0
Потому что du= -sin(x) dx. Производная косинуса равна минус синусу.
Автор ответа:
0
-sin(x) dx = du. Вот мы и заменили в исходном выражении.
Автор ответа:
0
Да, du = d(cos(x)) = -sin(x) dx. Замену же делали u=cos(x).
Автор ответа:
0
У меня при подстановке получилось (E^корень из 3/2 * 1/2) - E^1 * 0 = 1/2E^корень из 3 / 2
Автор ответа:
0
Интеграл равен минус е в степени косинус икс: (-e^cos(x)). Вместо икса подставляем x=pi/6=30 градусов, а затем x=0. В самом ответе так и написано.
Похожие вопросы
Предмет: Биология,
автор: murahaantonina
Предмет: Русский язык,
автор: jrjrkejejeie
Предмет: История,
автор: coolmotherstetes
Предмет: Математика,
автор: vopros2015