Предмет: Алгебра,
автор: NeSdalEGE
помогите решить №15 из ЕГЭ 2к17
Приложения:
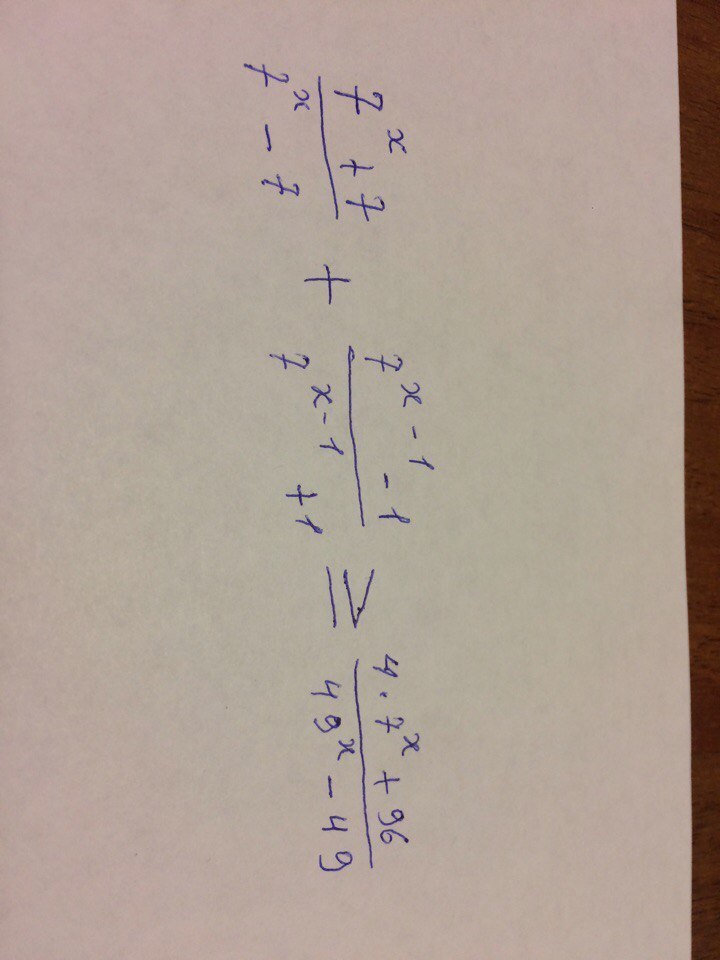
Ответы
Автор ответа:
0
умножаем второй на 7 числитель и знаменатель и приводим к общему знаменателю и переносим влево правую часть
переносим (7^x-7)(7^x+7)=(7^x)^2-49=49^x-49
отбрасываем 2/(7^x+7) как всегда больше 0
решаем по методу интервалов
------------ 0 -------------1 ++++++++++
x>1 x=0
Ответ x∈{0} U (1 +∞)
Похожие вопросы
Предмет: Алгебра,
автор: Evgeniy882
Предмет: Английский язык,
автор: samira22062009
Предмет: Русский язык,
автор: yurhenko01041979
Предмет: Обществознание,
автор: kirill182