Предмет: Математика,
автор: gallyamovdenis
Определите максимум функции
Приложения:
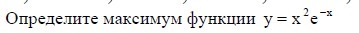
Ответы
Автор ответа:
2
Найдем производную:

y'=0 при x=0 и x=2
при этом:

Значит x=0 - точка минимума, x=2 - точка максимума.
Значение функции в точке максимума:

y'=0 при x=0 и x=2
при этом:
Значит x=0 - точка минимума, x=2 - точка максимума.
Значение функции в точке максимума:
Похожие вопросы
Предмет: История,
автор: nedocukelena
Предмет: Английский язык,
автор: krisstal08
Предмет: История,
автор: meridanilova3108
Предмет: Алгебра,
автор: vgfggfdfgghh
Предмет: Химия,
автор: mrglauzed