Предмет: Математика,
автор: kashezheva99
Помогите решить пожалуйста.
Найти производную функций:

Найти вторую производную функций:

NNNLLL54:
Удалят...
блин зря столько набирала чтоль. видела по 12 вопросов даже закидывали и ничего так ответы давали
значит те 12 вопросов удалят вместе с решением .
уже год они если не больше на этом сайте
ладно я как поняла не помогут
можно было и не многословить спасибо за помощь.
Это я тебе правила сайта пояснила, раз ты не прочитала их.
понятно все
Разбей хотя бы на 2 вопроса
Ответы
Автор ответа:
2
Автор ответа:
2
Применены формулы дифференцирования, свойства степени, формула квадрата суммы
Приложения:
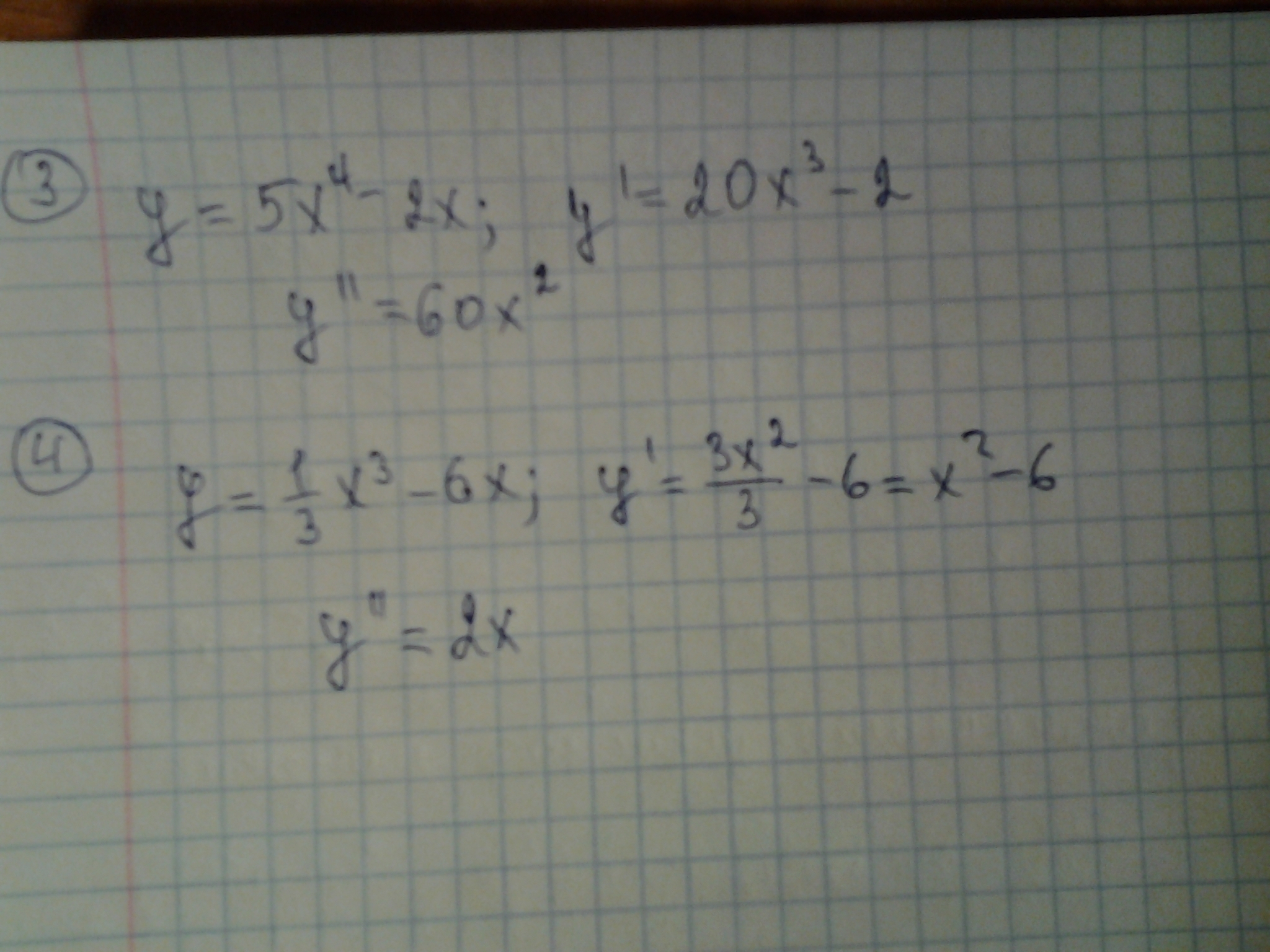
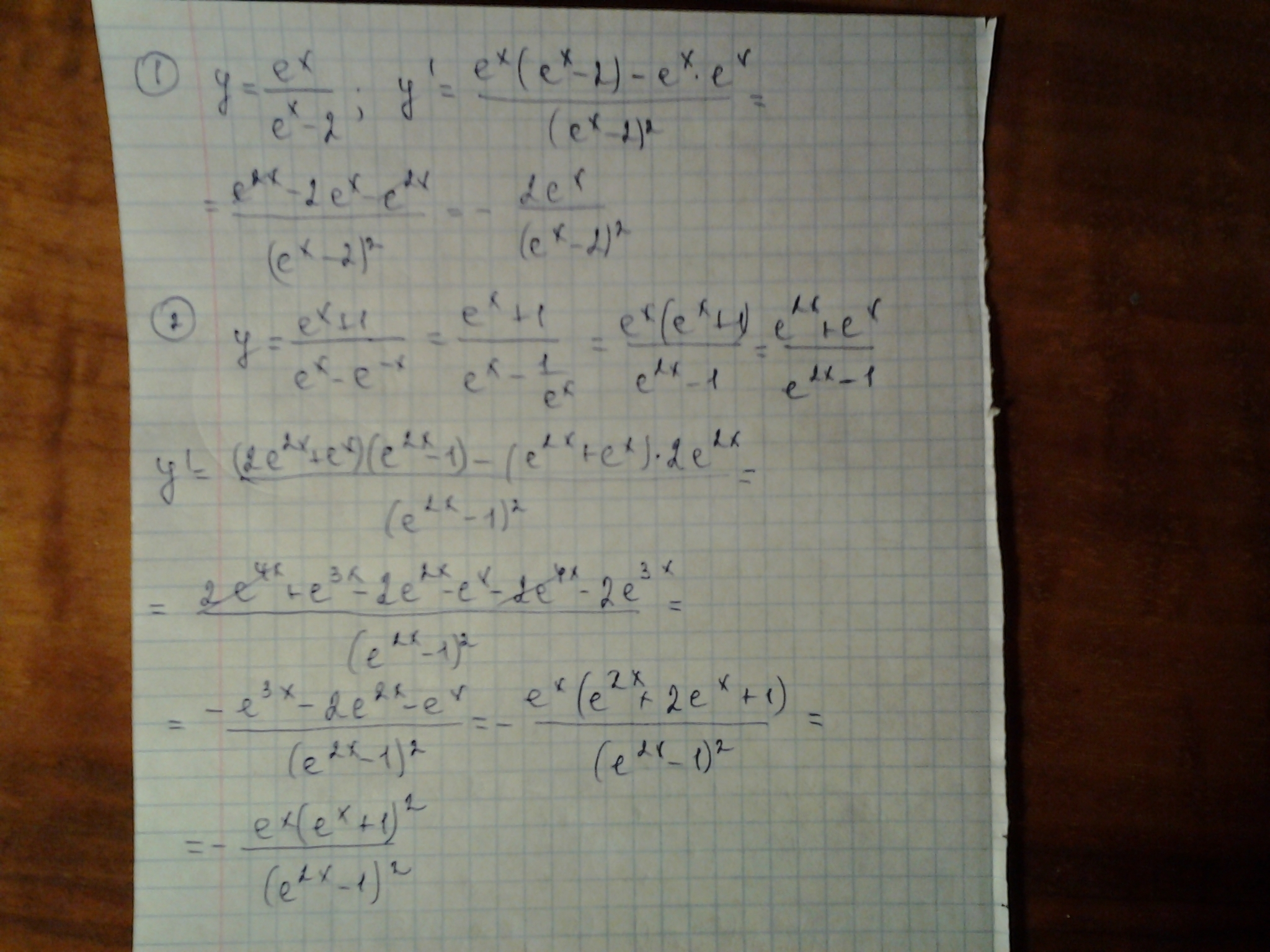
Похожие вопросы
Предмет: Математика,
автор: xaydarovf27
Предмет: Русский язык,
автор: elmarezimzade08
Предмет: Литература,
автор: vladasaltan
Предмет: Биология,
автор: qweyahfigjkf
Предмет: Алгебра,
автор: 12312412gaga