Предмет: Математика,
автор: natanatabob
Решить уравнение: cos^2(x)-cos(2x)=0,75 и найти все корни, принадлежащие промежутку [-2П;-П/2]
Ответы
Автор ответа:
0
cos²x - (2cos²x - 1) = 3/4
- cos²x + 1 = 3/4
cos²x = 1/4
cosx = 1/2 или cosx = - 1/2
x = π/3 + 2πn x = 2π/3 + 2πk
x = - π/3 + 2πm x = - 2π/3 + 2πl
Группы корней можно объединить:
x = π/3 + πn
x = - π/3 + πk
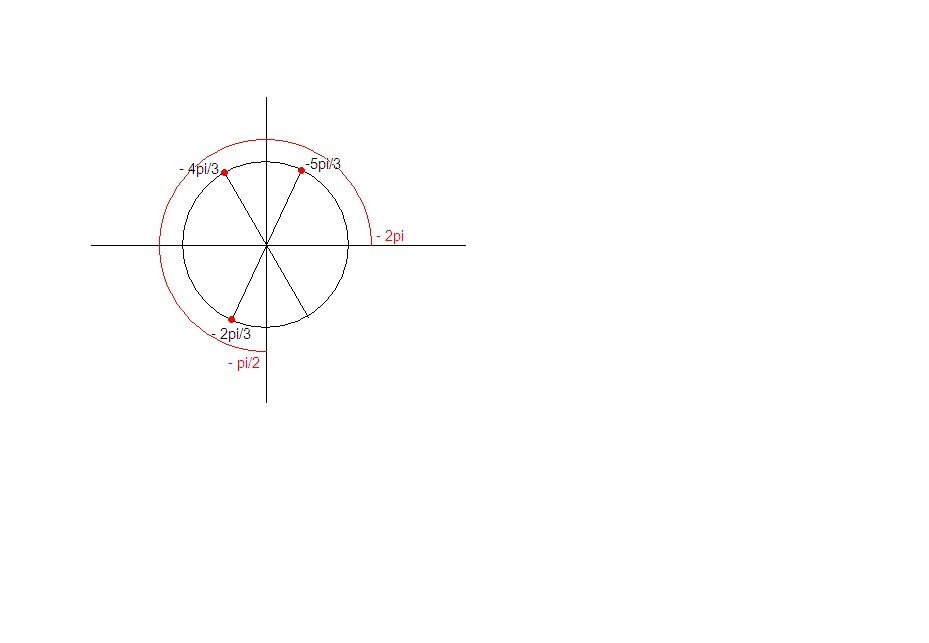
На промежуток [ - 2π ; - π/2] попали корни
- 2π/3; - 4π/3; - 5π/3
- cos²x + 1 = 3/4
cos²x = 1/4
cosx = 1/2 или cosx = - 1/2
x = π/3 + 2πn x = 2π/3 + 2πk
x = - π/3 + 2πm x = - 2π/3 + 2πl
Группы корней можно объединить:
x = π/3 + πn
x = - π/3 + πk
На промежуток [ - 2π ; - π/2] попали корни
- 2π/3; - 4π/3; - 5π/3
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: banantoperasyl
Предмет: Математика,
автор: hutornenkoaleksandr
Предмет: Химия,
автор: Abbaccio
Предмет: Русский язык,
автор: sashad2004
Предмет: Математика,
автор: nastya24566745677